Estadística descriptiva usando el Barómetro de las Américas (1)

Introducción

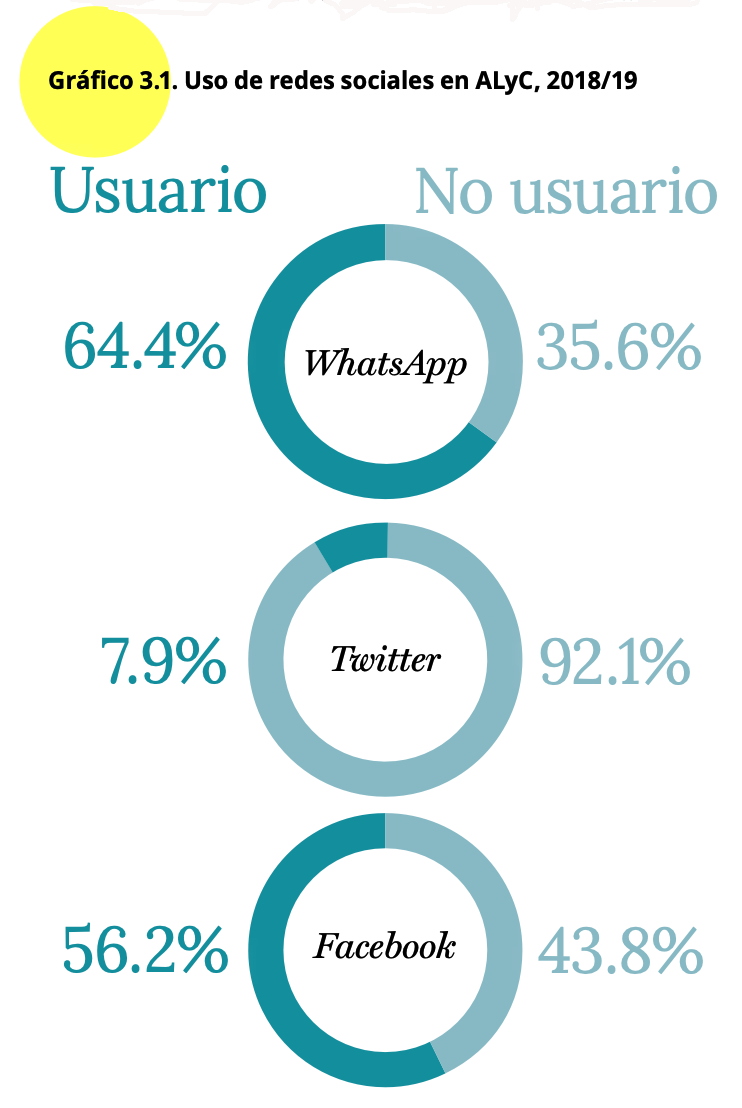
En este documento empezaremos con los aspectos básicos de cómo usar la base de datos del Barómetro de las Américas de LAPOP para fines estadísticos. En primer lugar, veremos aspectos básicos de cómo describir una variable mediante una tabla de distribución de frecuencias y cómo graficar esa variable mediante gráficos circulares o de barras. Para eso, vamos a usar el último informe regional “El pulso de la democracia”, disponible aquí, donde se presentan los principales hallazgos de la ronda 2018/19 del Barómetro de las Américas. Una de las secciones de este informe, reporta los datos sobre redes sociales y actitudes políticas. En esta sección, se presentan datos sobre el uso de internet y el uso de redes sociales, en general y por país. Con los datos del Barómetro de las Américas se puede saber el porcentaje de hogares con acceso a celulares, con acceso a internet, así como el porcentaje de personas que usa Whatsapp, Facebook o Twitter. En este documento vamos a reproducir estos resultados.

Sobre la base de datos

Los datos que vamos a usar deben citarse de la siguiente manera: Fuente: Barómetro de las Américas por el Proyecto de Opinión Pública de América Latina (LAPOP), wwww.LapopSurveys.org. En este documento se carga nuevamente desde cero una base de datos recortada. Se recomienda nuevamente limpiar el Environment de los objetos usados en módulos anteriores.

Esta base de datos se encuentra alojada en el repositorio “materials_edu” de la cuenta de LAPOP en GitHub. Mediante la librería rio y el comando import se puede importar esta base de datos desde este repositorio. Además, se seleccionan los datos de países con códigos menores o iguales a 35, es decir, se eliminan las observaciones de Estados Unidos y Canadá.

library(rio)
lapop18 <- import("https://raw.github.com/lapop-central/materials_edu/main/LAPOP_AB_Merge_2018_v1.0.sav")
lapop18 <- subset(lapop18, pais<=35)

También cargamos la base de datos de la ronda 2021.

lapop21 = import("lapop21.RData")
lapop21 <- subset(lapop21, pais<=35)

Apoyo a la democracia

En el reporte de El Pulso de la Democracia 2021 se presenta los resultados del apoyo a la democracia por país. El gráfico 1.1 muestra el porcentaje de personas en cada país que apoya a la democracia en abstracto.

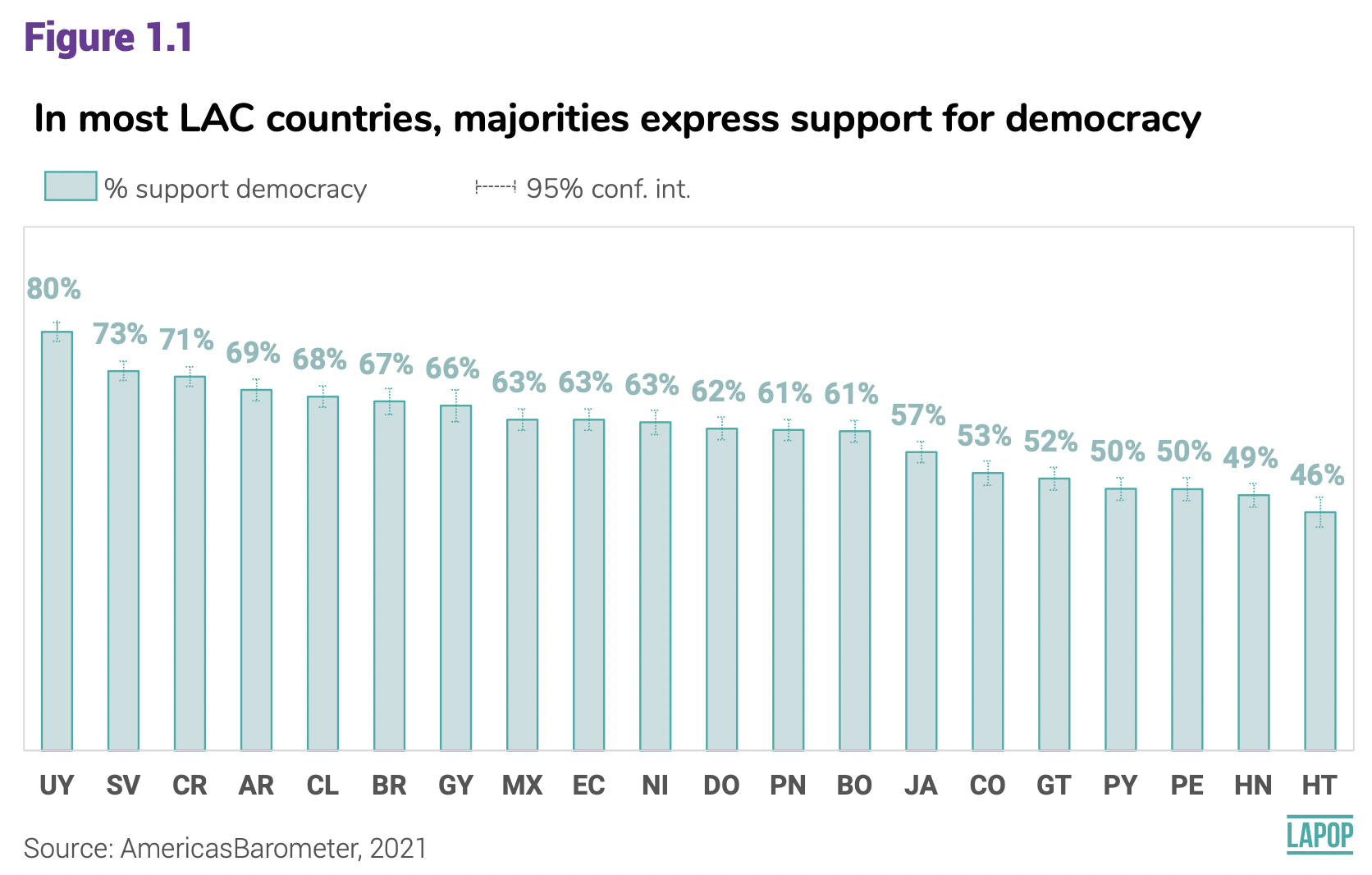
En los módulos anteriores se vio cómo recodificar la variable ING4, medida originalmente en una escala del 1 al 7, donde 1 significa “muy en desacuerdo” y 7 significa “muy de acuerdo”. Los valores entre 5 a 7 son recodificados como “1”, que identifica a aquellos que apoyan a la democracia. El resto se recodifica como “0”, aquellos que no apoyan a la democracia. Esta recodificación se guarda en una nueva variable “ing4rec”.

library(car)
lapop21$ing4rec <- car::recode(lapop21$ing4, "1:4=0; 5:7=1")

En sentido estricto, esta variable no es numérica, a pesar que está definida en la base de datos como “dbl”, que es un tipo de variable numérica. Esta variable es de tipo cualitativo, nominal, que en R se define como factor. Para tener correctamente definida y etiquetada esta variable, se tiene que transformar. En primer lugar se define como factor con el comando as.factor.

lapop21$ing4rec = as.factor(lapop21$ing4rec)

Una variable de tipo factor puede tener etiquetas por cada código numérico. La definición de etiquetas tiene el objetivo que en cualquier table o gráfico no aparezca el código numérico, sino la etiqueta correspondiente. Esto se hace usando el comando levels. Luego, esta variable se puede describir con el comando table, que nos brinda las frecuencias absolutas por cada categoría de la variable.

levels(lapop21$ing4rec) <- c("No", "Sí")
table(lapop21$ing4rec)

## 
##    No    Sí 
## 20523 36240

Describir la variable

Como vimos en el módulo sobre Manejo de Datos, se puede usar el comando prop.table para tener las frecuencias relativas y el comando round para mostrar solo un decimal.

round(prop.table(table(lapop21$ing4rec))*100, 1)

## 
##   No   Sí 
## 36.2 63.8

Este gráfico muestra los resultados de las 2 categorías definidas de la variable de apoyo a la democracia. Sin embargo, esta variable tiene valores perdidos. Para poder tener una tabla con los valores perdidos, se puede usar el comando table con la especificación useNA = "always".

round(prop.table(table(lapop21$ing4rec, useNA = "always"))*100, 1)

## 
##   No   Sí <NA> 
## 33.8 59.7  6.4

En esta tabla se ve que existe un 6.4% de casos perdidos del total de observaciones. La presentación de valores perdidos en tablas o gráficos depende del investigador.

Graficar la variable

Una variable de tipo “factor” se puede graficar de varias maneras. Una posibilidad es tener un gráfico circular. Se puede usar el comando pie que es parte de la sintaxis básica de R. Dentro de este comando se puede anidar el comando table para graficar estos valores.

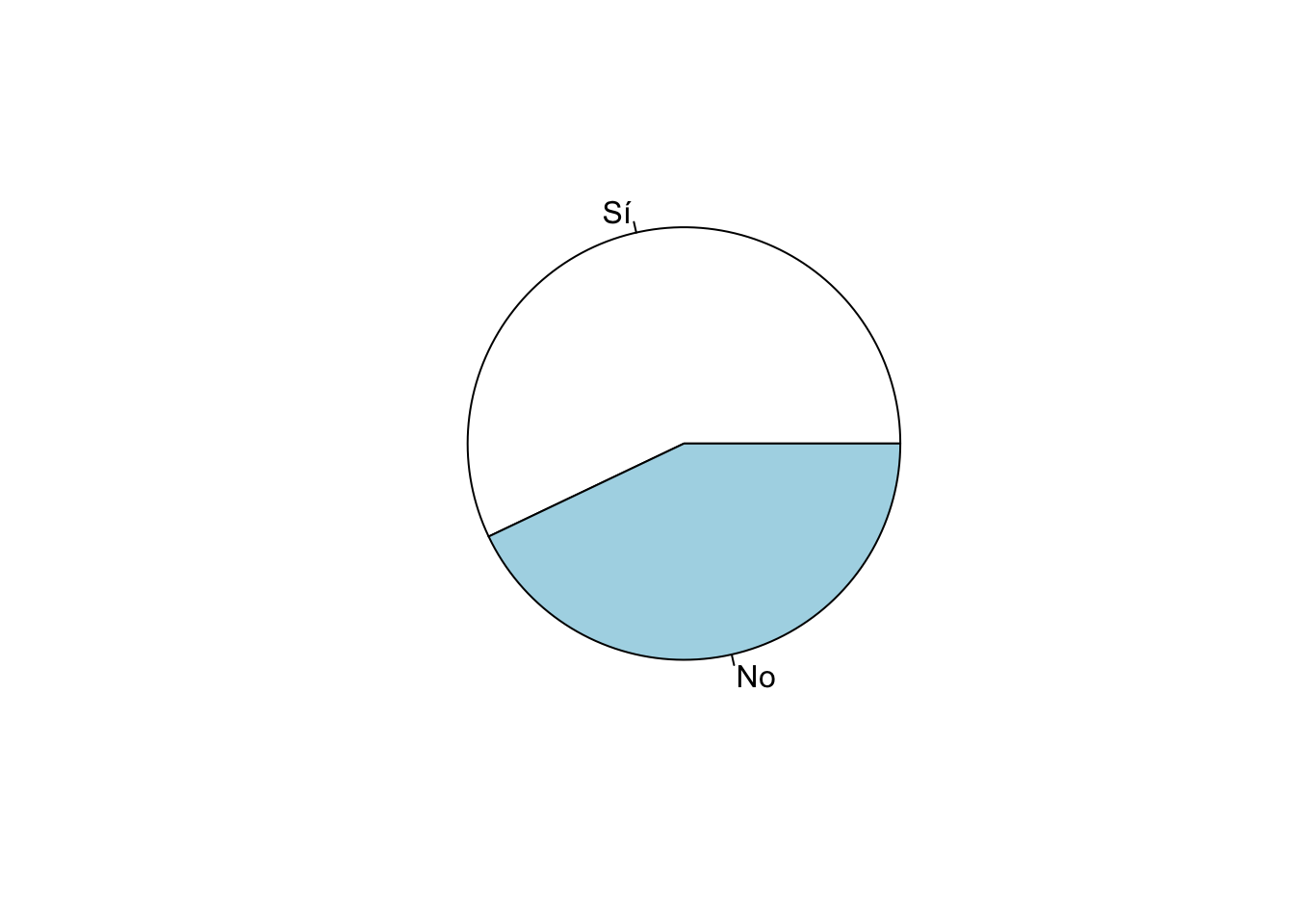
pie(table(lapop21$ing4rec))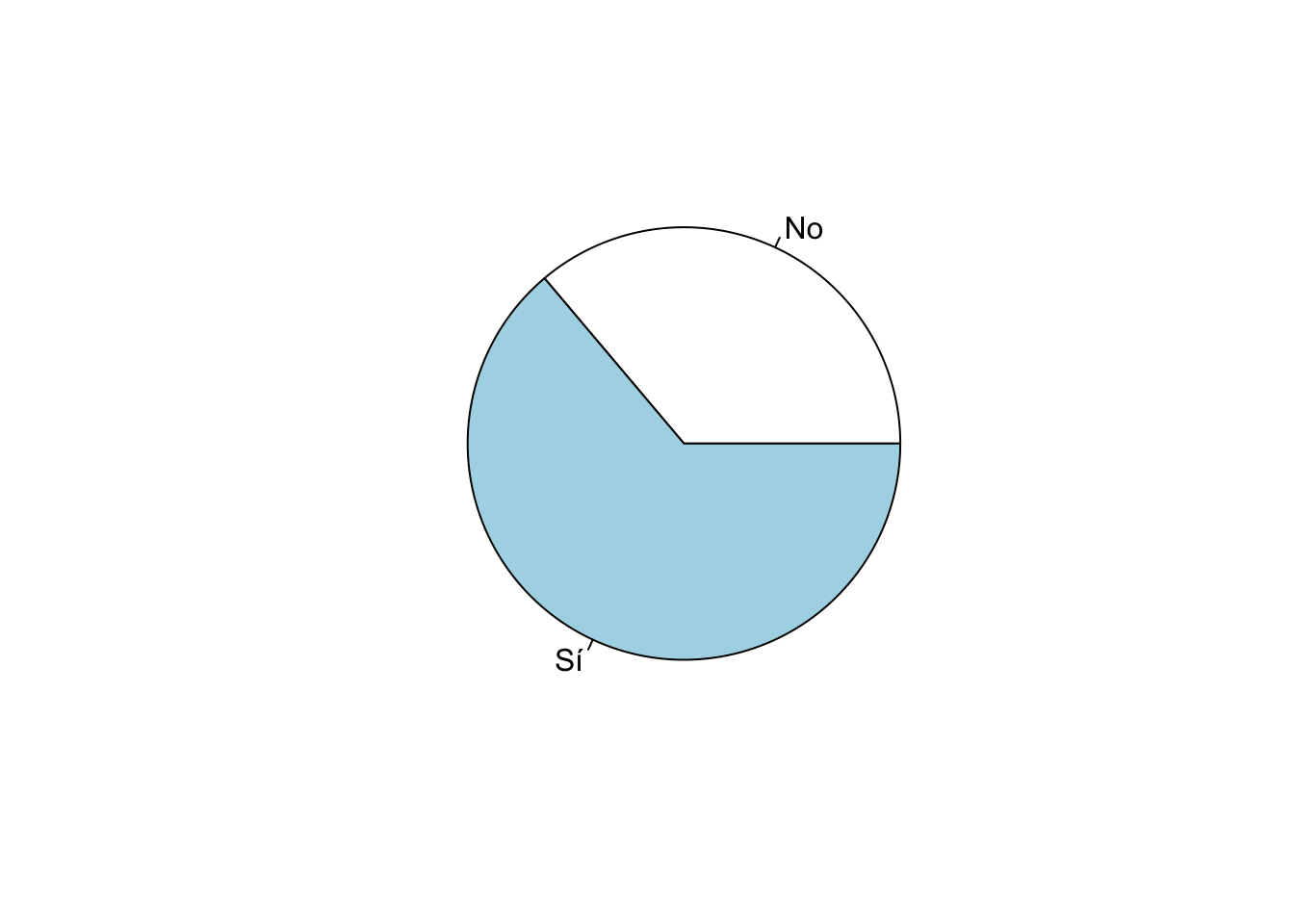

Este gráfico tiene algunas opciones de personalización. Por ejemplo, la especificación labels=… sirve para incluir el número de casos de cada sector y la especificación col=… sirve para definir los colores de los sectores.

pie(table(lapop21$ing4rec), labels=table(lapop21$ing4rec), col=1:2)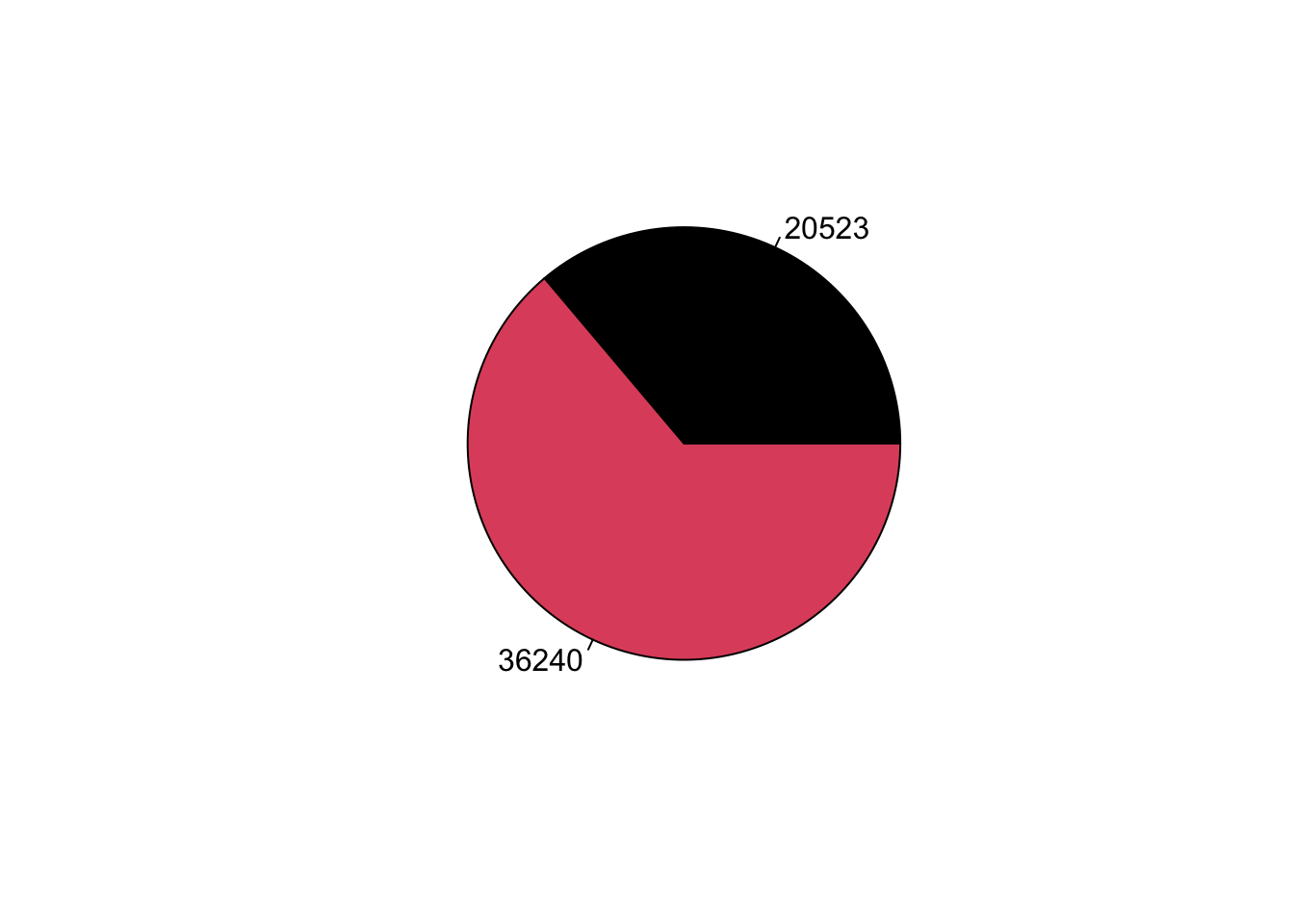

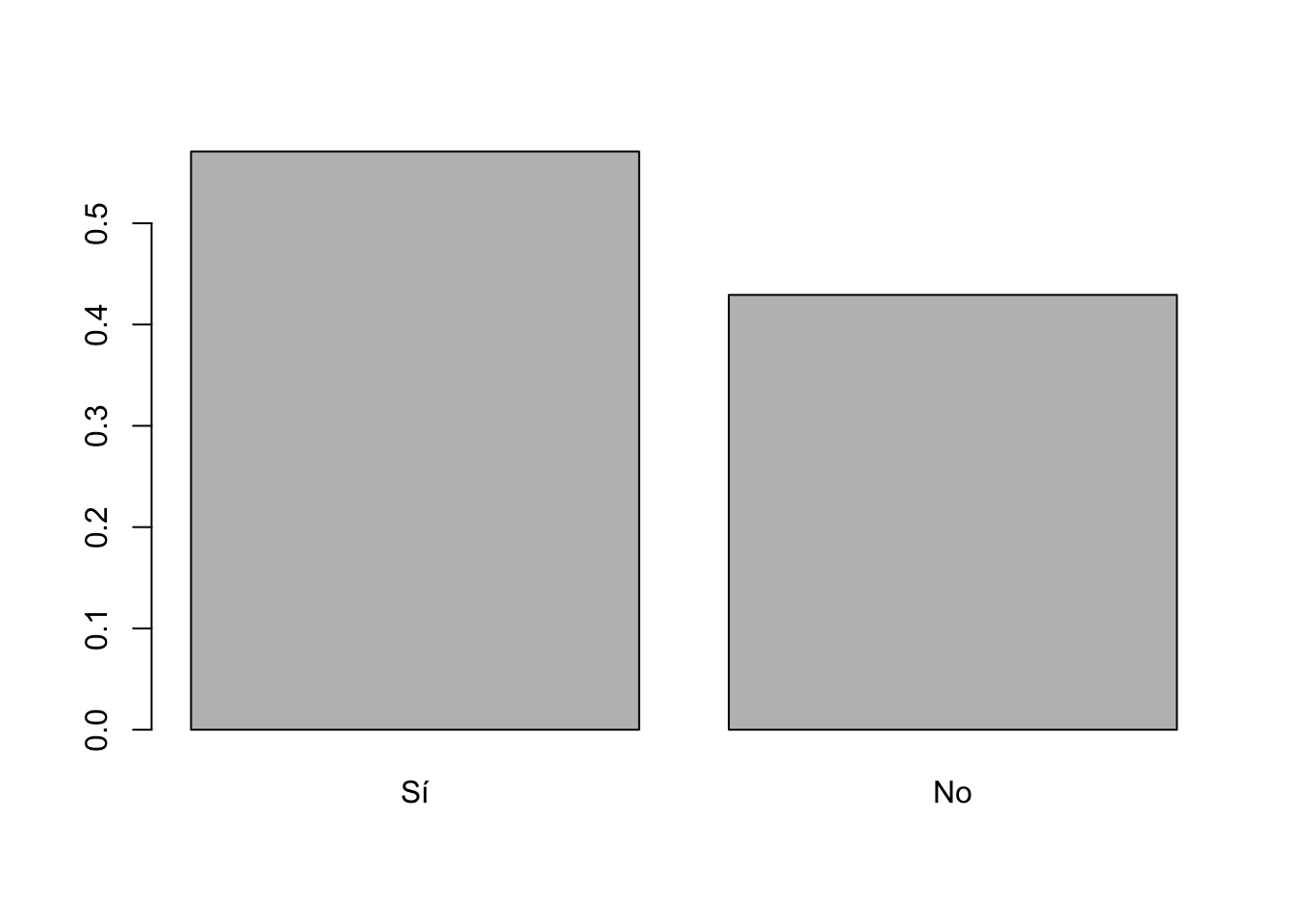
Otra opción es usar un gráfico de barras. Usando los comandos básicos de R, se puede usar el comando barplot.

barplot(prop.table(table(lapop21$ing4rec))*100, col=1:2)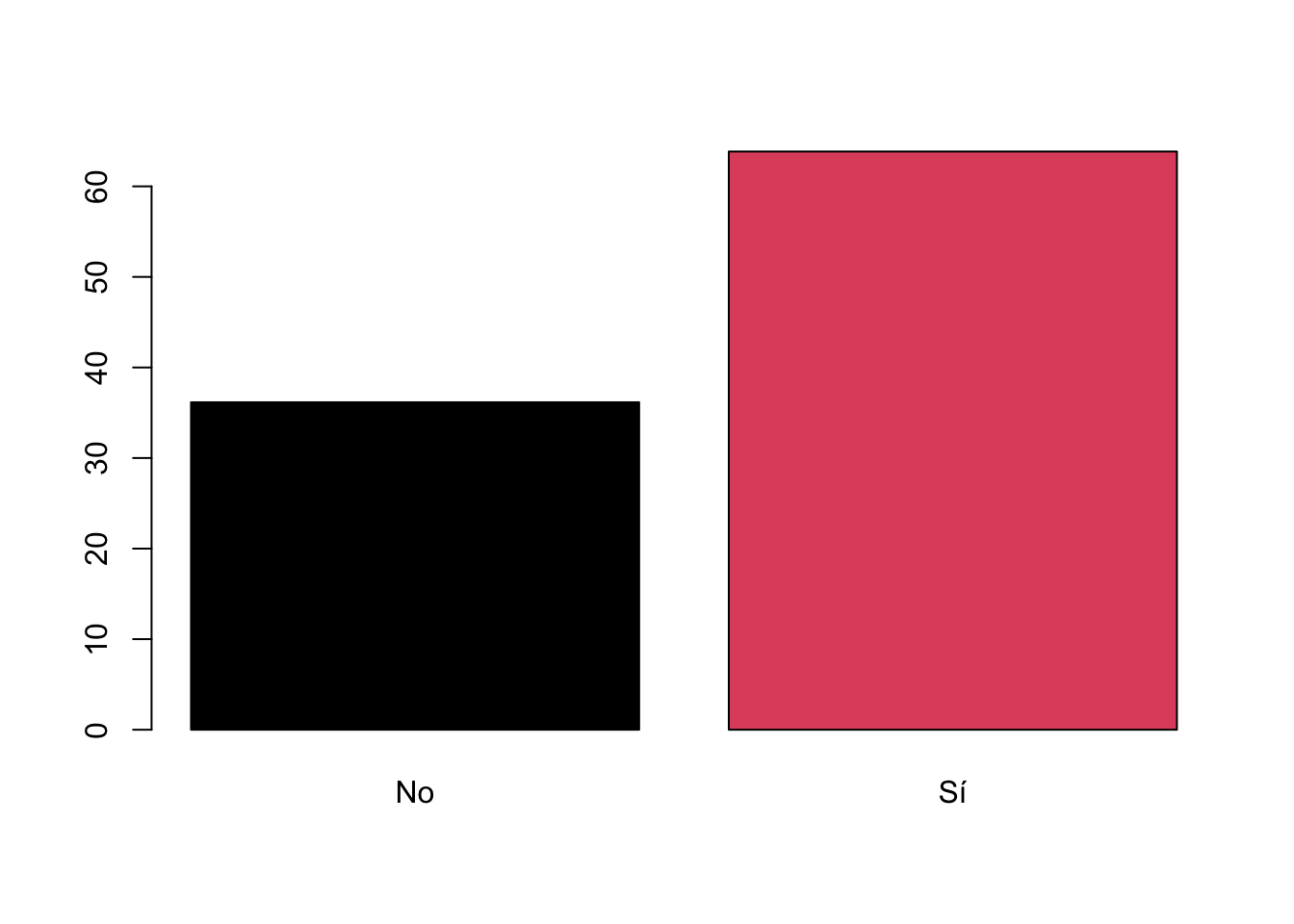

Los comando de base de R tienen un nivel de personalización, pero existe una librería especializada para hacer gráficos llamada ggplot con más opciones gráficas. Por ejemplo, para reproducir un gráfico de barras de la variable de apoyo a la democracia se llama a la librería ggplot2.

En este ejemplo lo primero que tenemos que definir son los datos que se van a usar con la especificación data=lapop. El comando ggplot trabaja sumando capas. La especificación aes sirve para definir la “estética” del gráfico. Generalmente se usa para indicar qué variable se va a graficar en qué eje (x o y). También se puede usar la especificación fill= para definir los grupos que se van a generar.

Luego de especificar los datos y los ejes, se tiene que especificar el tipo de gráfico que se quiere realizar. Esto se hace con las geometrías (“geom”). Se define un gráfico de barras simple, usando el comando geom_bar(), donde internamente se define el ancho de la barra. Con la especificación labs se define las etiquetas de ejes y el “caption”. Finalmente, con la especificación coord_cartesian se define los límites del eje Y de 0 a 80.

library(ggplot2)
ggplot(data=lapop21, aes(x=ing4rec))+
  geom_bar(aes(y=..prop..*100, group=1), width=0.5)+
  labs(x="Apoyo a la democracia", y="Porcentaje", 
       caption="Barómetro de las Américas por LAPOP, 2021")+
  coord_cartesian(ylim=c(0, 80))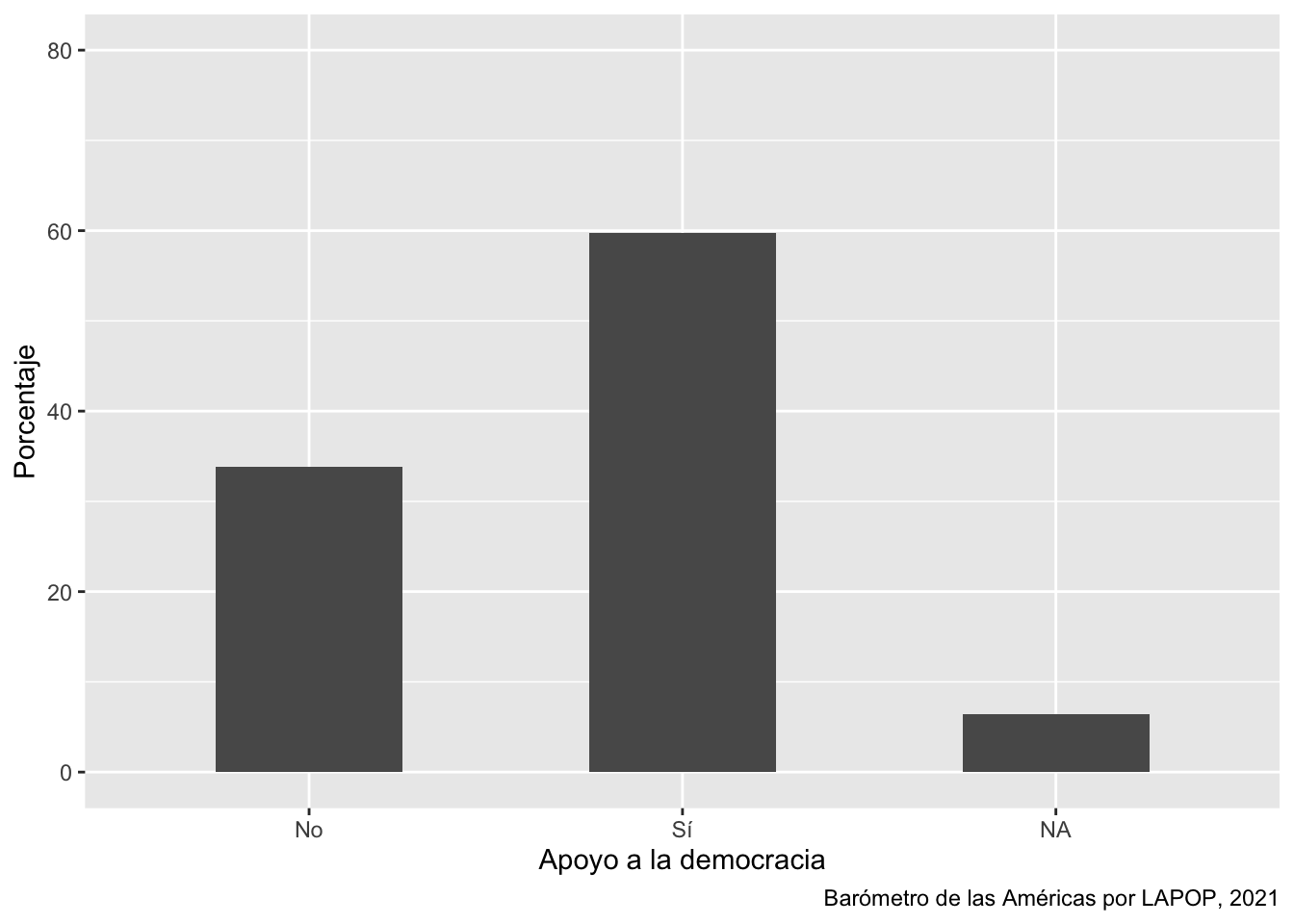

Tal como se definió el gráfico, se presenta una barra del porcentaje de casos perdidos. Si el investigador quisiera presentar un gráfico de porcentaje sobre el total de casos válidos, los casos perdidos deben ser eliminados. Se usa el comando subset nuevamente, pero dentro de ggplot para que el comando (internamente) trabaje con la variable pero sin considerar los valores perdidos. La sintaxis !is.na() hace que el comando no incluya los valores perdidos de una variable en los cálculos. Si se hubiera usado !is.na() fuera de ggplot creando una nueva variable, se hubieran eliminado todas las observaciones con valores perdidos, lo que disminuiría el N, afectando futuros cálculos.

ggplot(data=subset(lapop21, !is.na(ing4rec)), aes(x=ing4rec))+
  geom_bar(aes(y=..prop..*100, group=1), width=0.5)+
  labs(x="Apoyo a la democracia", y="Porcentaje", 
       caption="Barómetro de las Américas por LAPOP, 2021")+
  coord_cartesian(ylim=c(0, 80))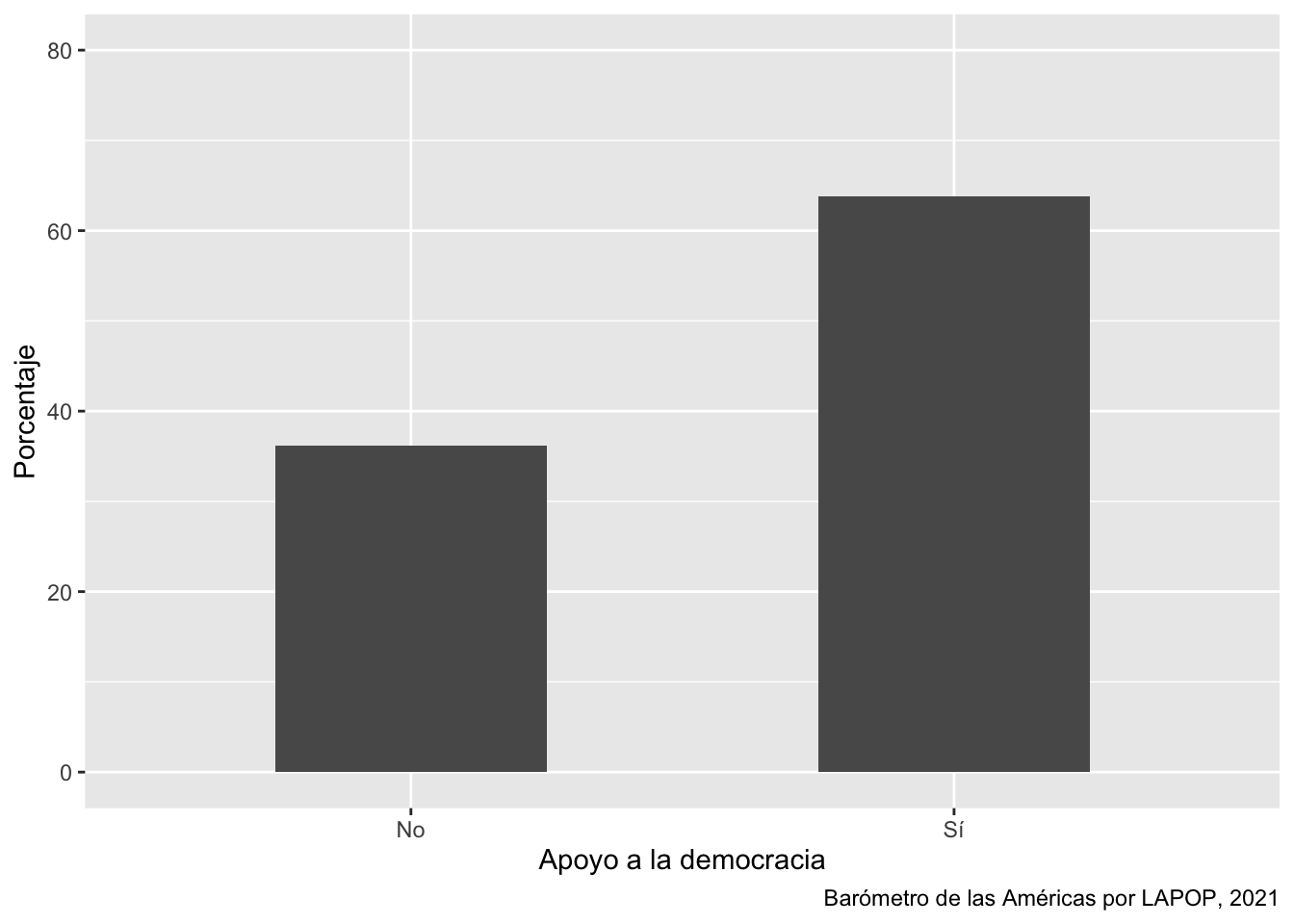

Hasta aquí se ha presentado un gráfico de barras de la variable apoyo a la democracia para toda la muestra, que incluye a todos los países. El gráfico 1.1 muestra el porcentaje que apoya a la democracia por país. Este tipo de gráfico se verá más adelante.

Usuarios de redes sociales

Ahora se usará un ejemplo del reporte El Pulso de la Democracia de la ronda 2018/19. Se seguirá procedimientos similares a la sección anterior y se replicarán algunos gráficos del mismo reporte de esa ronda. Las variables con las que se trabajará son: SMEDIA1. ¿Tiene usted cuenta de Facebook?; SMEDIA4. ¿Tiene usted cuenta de Twitter?; SMEDIA7. ¿Tiene usted cuenta de Whatsapp?. Estas preguntas tienen como opciones de respuesta:

1. Sí

2. No

Al momento de leer la base de datos en R, este programa importa las variables como “num”, que la mayoría de funciones en R trata como numéricas. Estas variables se tienen que convertir a variables de tipo “factor” con el comando as.factor, pues son variables categóricas. Esta nuevas variables las guardamos en el dataframe. Aquí se ha usado el operador = que es similar al operador <- que asigna un procedimiento a un nuevo objeto de un dataframe de R.

lapop18$smedia1r = as.factor(lapop18$smedia1)
lapop18$smedia4r = as.factor(lapop18$smedia4)
lapop18$smedia7r = as.factor(lapop18$smedia7)

Estas nuevas variables de tipo factor se tienen que etiquetar con el comando levels. Se usa un vector con las etiquetas concatenadas, usando el comando c().

levels(lapop18$smedia1r) <- c("Sí", "No")
levels(lapop18$smedia4r) <- c("Sí", "No")
levels(lapop18$smedia7r) <- c("Sí", "No")

Calcular las variables de usuarios de redes sociales

Como vimos en un módulo anterior, se puede calcular nuevas variables con valores condicionales de otras variables usando el comando ifelse. De esta manera, se crea las variables de usuarios de redes sociales.

lapop18$fb_user <- ifelse(lapop18$smedia1==1 & lapop18$smedia2<=4, 1, 0)
lapop18$tw_user <- ifelse(lapop18$smedia4==1 & lapop18$smedia5<=4, 1, 0)
lapop18$wa_user <- ifelse(lapop18$smedia7==1 & lapop18$smedia8<=4, 1, 0)

Describir las variables

Con las variables listas, ahora procedemos a hacer las tablas generales con el comando table. Se puede notar el uso de # como forma de hacer anotaciones, que no son código en R.

table(lapop18$smedia1r) #Facebook

## 
##    Sí    No 
## 15389 11573

table(lapop18$smedia4r) #Twitter

## 
##    Sí    No 
##  2363 24558

table(lapop18$smedia7r) #Whatsapp

## 
##    Sí    No 
## 17446  9569

Este comando table nos brinda las frecuencias absolutas (número de observaciones) por cada categoría de las variables (en este caso Sí y No). Para obtener las frecuencias relativas, usaremos el comando prop.table, donde se anida el comando anterior table.

prop.table(table(lapop18$smedia1r))

## 
##        Sí        No 
## 0.5707663 0.4292337

prop.table(table(lapop18$smedia4r))

## 
##         Sí         No 
## 0.08777534 0.91222466

prop.table(table(lapop18$smedia7r))

## 
##        Sí        No 
## 0.6457894 0.3542106

Sin embargo, el comando prop.table nos devuelve demasiados decimales y las frecuencias relativas en una escala de 0 a 1. Para redondear esta cifra usamos el comando round, que nos permite especificar el número de decimales que se quiere mostrar. Tanto el comando table, como prop.table se anidan dentro de este nuevo comando. En este caso se ha usado 3 decimales, para cuando se multiplique por 100, quede en forma de porcentaje con 1 decimal.

round(prop.table(table(lapop18$smedia1r)), 3)*100

## 
##   Sí   No 
## 57.1 42.9

round(prop.table(table(lapop18$smedia4r)), 3)*100

## 
##   Sí   No 
##  8.8 91.2

round(prop.table(table(lapop18$smedia7r)), 3)*100

## 
##   Sí   No 
## 64.6 35.4

No es práctico presentar 3 tablas cuando las variables tienen las mismas categorías de respuesta. Para fines de presentación podría ser mejor construir una sola tabla. Se puede guardar las tablas parciales en nuevos objetos con el operador <- y luego unirlas como filas con el comando rbind en un nuevo dataframe “tabla”, de tal manera que las respuestas a cada red social aparezcan en filas.

Facebook <- round(prop.table(table(lapop18$smedia1r)), 3)*100
Twitter <- round(prop.table(table(lapop18$smedia4r)), 3)*100
Whatsapp <- round(prop.table(table(lapop18$smedia7r)), 3)*100
tabla <- as.data.frame(rbind(Facebook, Twitter, Whatsapp))
tabla

##            Sí   No
## Facebook 57.1 42.9
## Twitter   8.8 91.2
## Whatsapp 64.6 35.4

Para tener una mejor presentación de la tabla, se puede usar el comando kable del paquete knitr, usando la tabla construida anteriormente.

library(knitr)
knitr::kable(tabla, format="markdown")

	Sí	No
Facebook	57.1	42.9
Twitter	8.8	91.2
Whatsapp	64.6	35.4

Graficar las variables

En el Gráfico 3.1 del reporte se observa que se reportan estos datos mediante un gráfico de sectores circulares.

Se puede reproducir ese gráfico usando el comando pie que es parte de la sintaxis básica de R. Dentro de este comando se puede anidar el comando table para graficar estos valores.

pie(table(lapop18$smedia1r))

También se podría pensar en un gráfico de barras. Usando los comandos básicos de R, se puede usar el comando barplot.

barplot(prop.table(table(lapop18$smedia1r)))

Estos comandos gráficos tienen opciones para adecuar el gráfico, por ejemplo, para incluir los porcentajes y adecuar las escalas. Pero, para tener más opciones gráficas, podemos usar el paquete ggplot para reproducir el gráfico circular.

En este ejemplo lo primero que tenemos que definir son los datos que se van a usar. Se ha usado el comando subset nuevamente, pero dentro de ggplot para que el comando (internamente) trabaje con la variable pero sin los valores perdidos. La sintaxis !is.na() hace que el comando no incluya los valores perdidos de una variable en los cálculos. Si se hubiera usado data=lapop el gráfico hubiera incluido un gran sector correspondiente a la proporción de NA. Si se hubiera usado !is.na() fuera de ggplot creando una nueva variable, se hubieran eliminado todas las observaciones con valores perdidos, lo que disminuiría el N, afectando futuros cálculos.

El comando ggplot trabaja sumando capas. La especificación aes sirve para definir la “estética” del gráfico. Generalmente se usa para indicar qué variable se va a graficar en qué eje (x o y). También se puede usar la especificación fill= para definir los grupos que se van a generar.

Luego de especificar los datos y los ejes, se tiene que especificar el tipo de gráfico que se quiere realizar. Esto se hace con las geometrías (“geom”). No existe una geometría directa para hacer un gráfico circular, por lo que se tiene que usar inicialmente un gráfico de barras simple, usando el comando geom_bar(), donde internamente se define el ancho de la barra. Si dejáramos la sintaxis en este punto, se generaría una barra que se dividiría entre los valores de la variable “smedia1r”. Para genera el gráfico circular, se tiene que agregar otro comando coord_polar, que transforma la barra a coordenadas polares, creando un gráfico circular.

library(ggplot2) #librería especializada en gráficos
ggplot(data=subset(lapop18, !is.na(smedia1r)), aes(x="", fill=smedia1r))+
  geom_bar(width=1) +
  coord_polar("y", start=0)

El gráfico anterior ha partido desde el mismo dataframe “lapop18”, usando los datos de “smedia1r”. Sin embargo, para manipular mejor el gráfico es más fácil crear un nuevo dataframe con los datos agregados (frecuencia y %). Es decir, guardar en un nuevo dataframe los datos de resultados de la tabla de “smedia1r”. Luego se usa ese nuevo dataframe para hacer el pie con ggplot.

Un aspecto a resaltar es que en este caso se está usando el tidyverse, que incluye el comando pipe %>% de la librería dplyr, que es una forma (un poco) diferente de escribir códigos en R, de manera concatenada, paso a paso. Una explicación simple de cómo se usa el pipe se puede encontrar aquí.

Lo primero que hay que notar es que se va a crear un nuevo objeto llamado “df”. En este objeto se va a guardar información que viene del dataframe “lapop18”. Se usa el comando subset para eliminar los valores perdidos de “smedia1r” del cálculo de los porcentajes. Luego (%>%), estos datos se van a agrupar por categorías de la variable “smedia1r”. A continuación (%>%), en cada grupo se calcula el total de observaciones con el comando summarise(n = n()). Finalmente (último paso con %>%), con este total por grupos se calcula los porcentajes y se guarda estos porcentajes en una nueva columna “per”.

library(dplyr)
df <- subset(lapop18, !is.na(smedia1r)) %>%
      group_by(smedia1r) %>% 
      dplyr::summarise(n = n()) %>%
      mutate(per=round(n/sum(n), 3)*100)
df

## # A tibble: 2 × 3
##   smedia1r     n   per
##   <fct>    <int> <dbl>
## 1 Sí       15389  57.1
## 2 No       11573  42.9

Con esta sintaxis se crea una tabla donde se tiene el total de observaciones y el porcentaje por cada categoría de la variable “smedia1r”. Una forma más directa de crear los mismos datos es usando la librería janitor y el comando tabyl. En R existen múltiples maneras de llegar a los mismos resultados.

library(janitor)
subset(lapop18, !is.na(smedia1r)) %>%
  tabyl(smedia1r)

##  smedia1r     n   percent
##        Sí 15389 0.5707663
##        No 11573 0.4292337

Una vez que tenemos la tabla, podemos usarla para trabajar el gráfico circular con ggplot. Nótese que en este caso los datos que se usan vienen del dataframe df (no de lapop18). Este dataframe tiene una columna llamada “per” con los porcentajes respectivos que se grafican en el eje Y. Igual que en el caso anterior, para hacer el gráfico circular, se parte del gráfico de barras (por eso geom_bar), que luego se pasa a coordenadas polares (por eso coord_polar).

Se agrega una capa de texto, con la especificación geom_text. Dentro de esta especificación se determina una “estética” con la etiqueta del dato aes(label=...), donde se junta con el comando paste el dato del porcentaje “per” y el símbolo “%”, con un espacio (sep=...) entre ellos. Se establece el color de la fuente con color="...". Se ajusta a blanco para que contraste con los colores del gráfico circular. Con el comando hjust=... se ajusta la posición horizontal de este texto. El comando ggplot puede incluir varios “temas” para el gráfico. En este caso se ha usado theme_void() que indica un fondo vacío. Finalmente, con la especificación scale_fill_discrete(name=...) se puede cambiar el título de la leyenda para que no aparezca el nombre de la variable, sino una etiqueta más adecuada.

ggplot(data=df, aes(x="", y=per, fill=smedia1r))+
  geom_bar(width=1, stat="identity")+
  geom_text(aes(label=paste(per, "%", sep="")), color="white",
            position=position_stack(vjust=0.5), size=3)+
  coord_polar("y")+
  theme_void()+
  scale_fill_discrete(name="¿Usa Facebook?")

Si en lugar de un gráfico circular se quiere presentar un gráfico de barras, con los datos del dataframe “lapop18” se puede utilizar el siguiente código. A diferencia del primer gráfico circular, ahora la especificación aes(..) incluye la variable “smedia1r” como variable a graficar en el eje X. Dentro del objeto geométrico geom_bar() se indica que la barra debe representar las proporciones en porcentajes aes(y=..prop..*100, group=1). En este ejemplo, se ha incluido un etiqueta general para el gráfico y para los ejes con el comando labs(...). En este comando también se puede agregar un “caption” para indicar la fuente de los datos. Finalmente, con la especificación coord_cartesian(ylim=c(0,60)) se limita el eje Y a valores entre 0 y 60.

ggplot(data=subset(lapop18, !is.na(smedia1r)), aes(x=smedia1r))+
  geom_bar(aes(y=..prop..*100, group=1), width=0.5)+
  labs(title="¿Qué tan frecuente se usan las redes sociales?", x="Usuario de Facebook", y="Porcentaje", caption="Barómetro de las Américas por LAPOP, 2018/19")+
  coord_cartesian(ylim=c(0, 60))

En este caso también se puede usar los datos agrupados del dataframe “df”. A diferencia de la opción anterior, en “df” se cuenta con el dato del porcentaje, por lo que no se debe calcular en el código, por lo que en la especificación de la estética indica que en el eje X se debe mostrar las alternativas de la variable “smedia1r” y en el eje Y el porcentaje, de esta manera aes(x=media1r, y=per). Por este motivo también en la especificación geom_bar, ahora en lugar de requerir el cálculo del porcentaje, solo se indica que replique los datos (con stat="identity") de aes. Finalmente, en este caso le agregamos la capa de texto para incluir los porcentajes en cada columna, con la especificación geom_text.

ggplot(df, aes(x=smedia1r, y=per))+
  geom_bar(stat="identity",  width=0.5)+
  geom_text(aes(label=paste(per, "%", sep="")), color="black", vjust=-0.5)+
  labs(title="¿Qué tan frecuente se usan las redes sociales?", x="Usuario de Facebook", y="Porcentaje", caption="Barómetro de las Américas por LAPOP, 2018/19")+
  coord_cartesian(ylim=c(0, 60))

Resumen

En este documento se ha trabajado con variables categóricas nominales, como si usa o no usa redes sociales. Se ha presentando las formas de cómo describir en tablas de frecuencia y cómo graficar estas variables, mediante gráficos circulares o de barras.

Cálculos incluyendo el efecto de diseño

Estos últimos resultados de la ronda 2018/19 no son exactamente iguales a los del reporte pues LAPOP incluye el efecto del diseño muestral en sus cálculos. Según esta sintaxis, se encuentra que el 57.1% de entrevistados reporta ser usuario de Facebook, cuando en el reporte aparece 56.2%. Lo mismo con Twitter, que aquí se calcula en 8.8% y en el reporte 7.9%; y con Whatsapp que aquí aparece con 64.6% y en el reporte con 64.4%. Como se indicó en el documento sobre el uso de los factores de expansión usando los datos del Barómetro de las Américas (disponible aquí), hay varias maneras de reproducir los resultados incorporando el efecto de diseño. Una primera opción es usar el comando freq que permite la inclusión de una variable de factor de expansión, como “weight1500”. Se incluye la especificación plot=F para no producir los gráficos de barras.

library(descr)
descr::freq(lapop18$fb_user, lapop18$weight1500, plot = F)

## lapop18$fb_user 
##       Frequency Percent Valid Percent
## 0         11337  41.988         43.77
## 1         14564  53.939         56.23
## NA's       1100   4.073              
## Total     27000 100.000        100.00

descr::freq(lapop18$tw_user, lapop18$weight1500, plot = F)

## lapop18$tw_user 
##       Frequency Percent Valid Percent
## 0         23819  88.220        92.023
## 1          2065   7.647         7.977
## NA's       1116   4.133              
## Total     27000 100.000       100.000

descr::freq(lapop18$wa_user, lapop18$weight1500, plot = F)

## lapop18$wa_user 
##       Frequency Percent Valid Percent
## 0          9252  34.266         35.63
## 1         16714  61.903         64.37
## NA's       1035   3.832              
## Total     27000 100.000        100.00

Sin considerar el efecto de diseño, se tiene que 57.1% de entrevistados cuenta con una cuenta de Facebook. Este porcentaje varía a 55.2% si se incluye la variable de expansión, que es el valor que se muestra en el reporte. Estos resultados ponderados también se pueden guardar en objetos y luego graficar de la misma manera que se ha hecho con los resultados sin ponderar.

Para el caso de Facebook, la tabla se puede guardar como un dataframe, usando el comando as.data.frame. Esta tabla incluye datos que no requerimos, como la fila de NA´s y del total y como la columna de Percent. Estas filas y esta columna se borran usando la especificación [-c(3,4), -2].

Luego, se le cambia el nombre a las columnas para evitar el nombre “Valid Percent”. Se las nombre simplemente como “freq” y “per”. Esta columna “per” es la que tiene los datos que graficaremos. Finalmente, se añade una columna “lab” con las etiquetas de cada fila de resultados.

fb <- as.data.frame(descr::freq(lapop18$fb_user, lapop18$weight1500, plot = F))
fb = fb[-c(3,4), -2]
colnames(fb) = c("freq", "per")
fb$lab = c("No", "Sí")
fb

##       freq      per lab
## 0 11336.69 43.77052  No
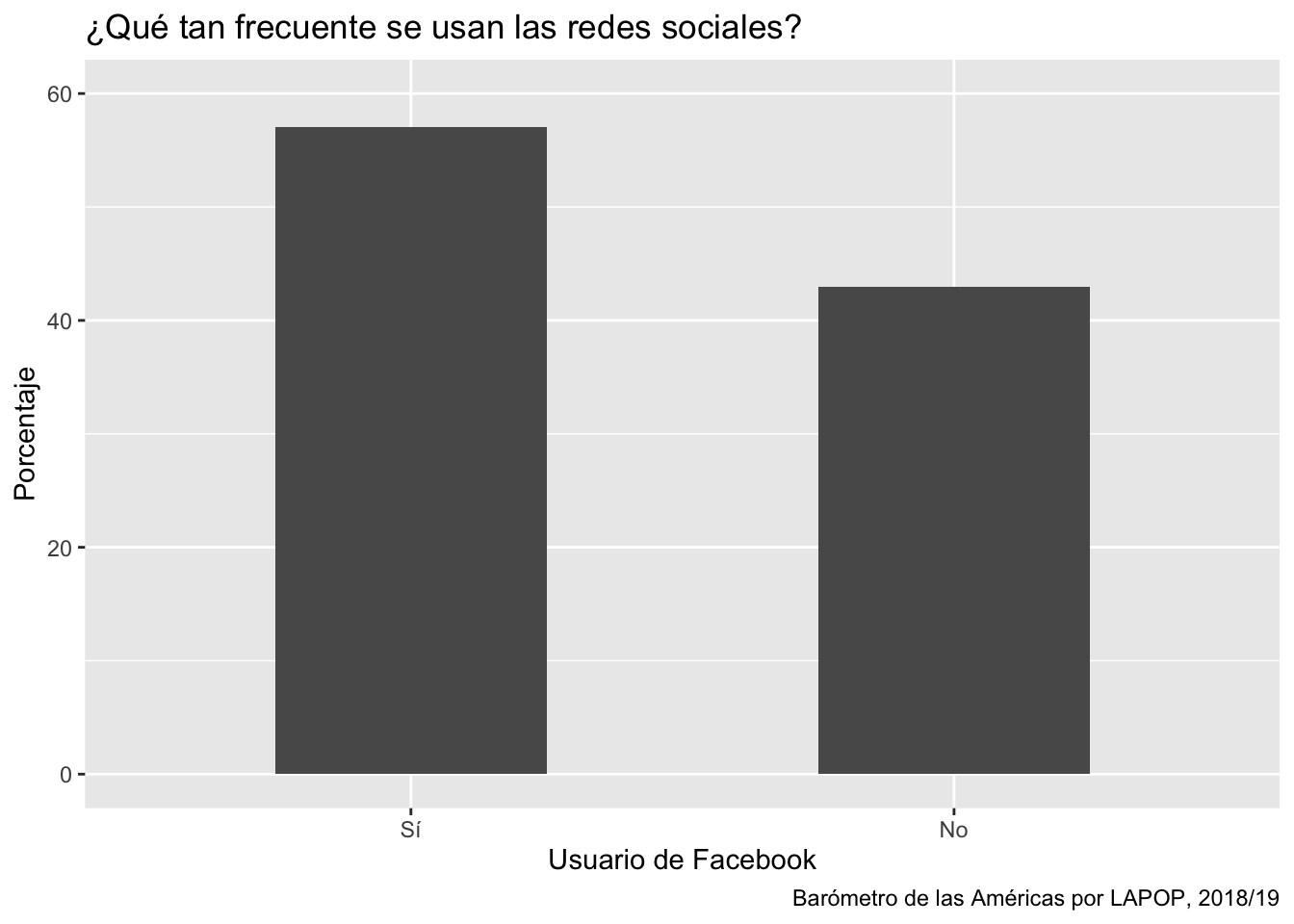
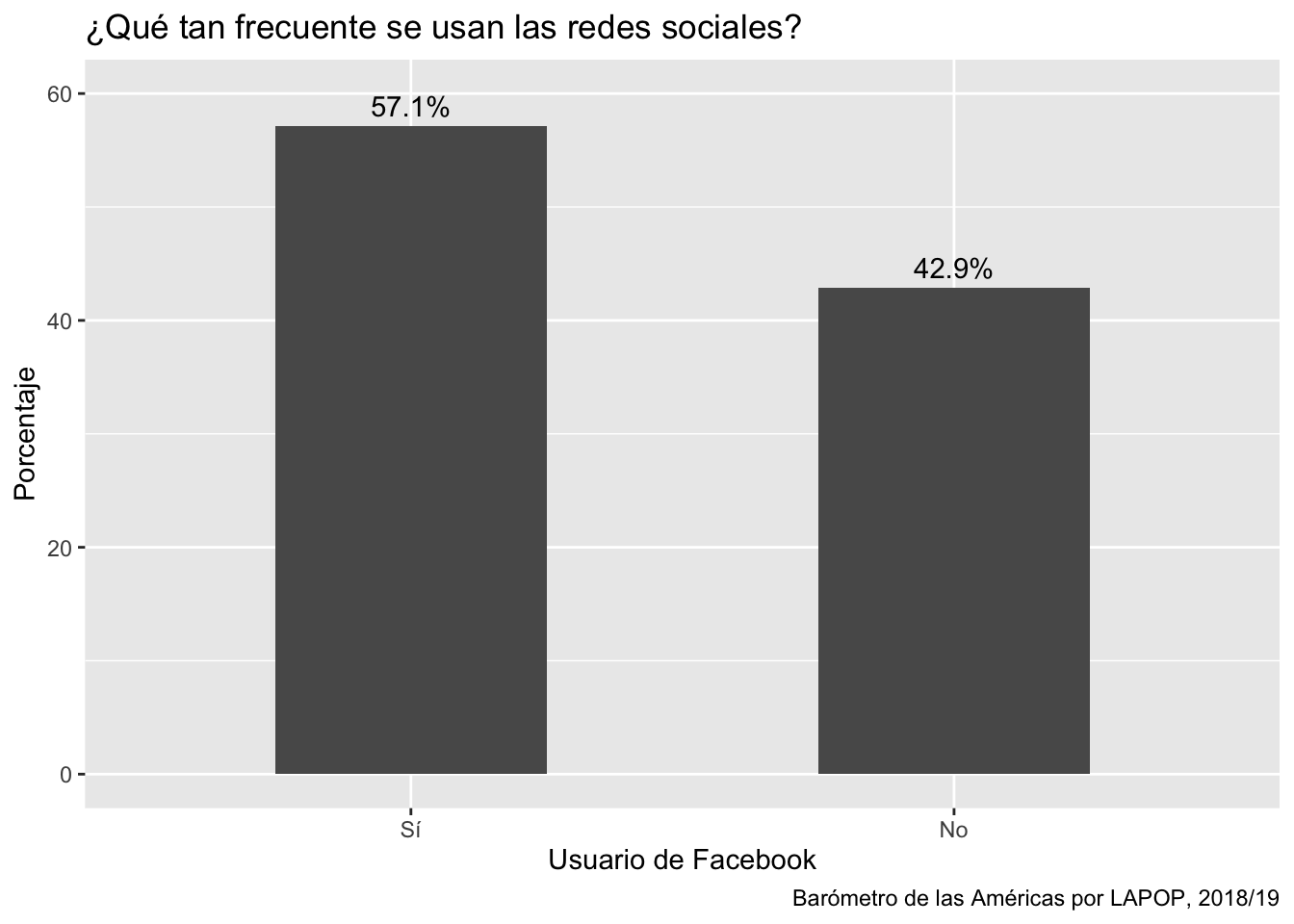
## 1 14563.60 56.22948  Sí

Con este nuevo dataframe podemos replicar los mismo códigos usados más arriba para hacer un gráfico de barras o un gráfico circular. El siguiente código muestra el gráfico de barras. Nótese que ahora se usa el dataframe “fb” y que en aes se especifica que en el eje X deben estar los datos de la columna “lab” y en el eje Y los datos de la columna “per”.

ggplot(data=fb, aes(x=lab, y=per))+
  geom_bar(stat="identity",  width=0.5)+
  geom_text(aes(label=paste(round(per, 1), "%", sep="")), color="black", vjust=-0.5)+
  labs(title="¿Qué tan frecuente se usan las redes sociales?", x="Usuario de Facebook", 
       y="Porcentaje", caption="Barómetro de las Américas por LAPOP, 2018/19")+
  coord_cartesian(ylim=c(0, 60))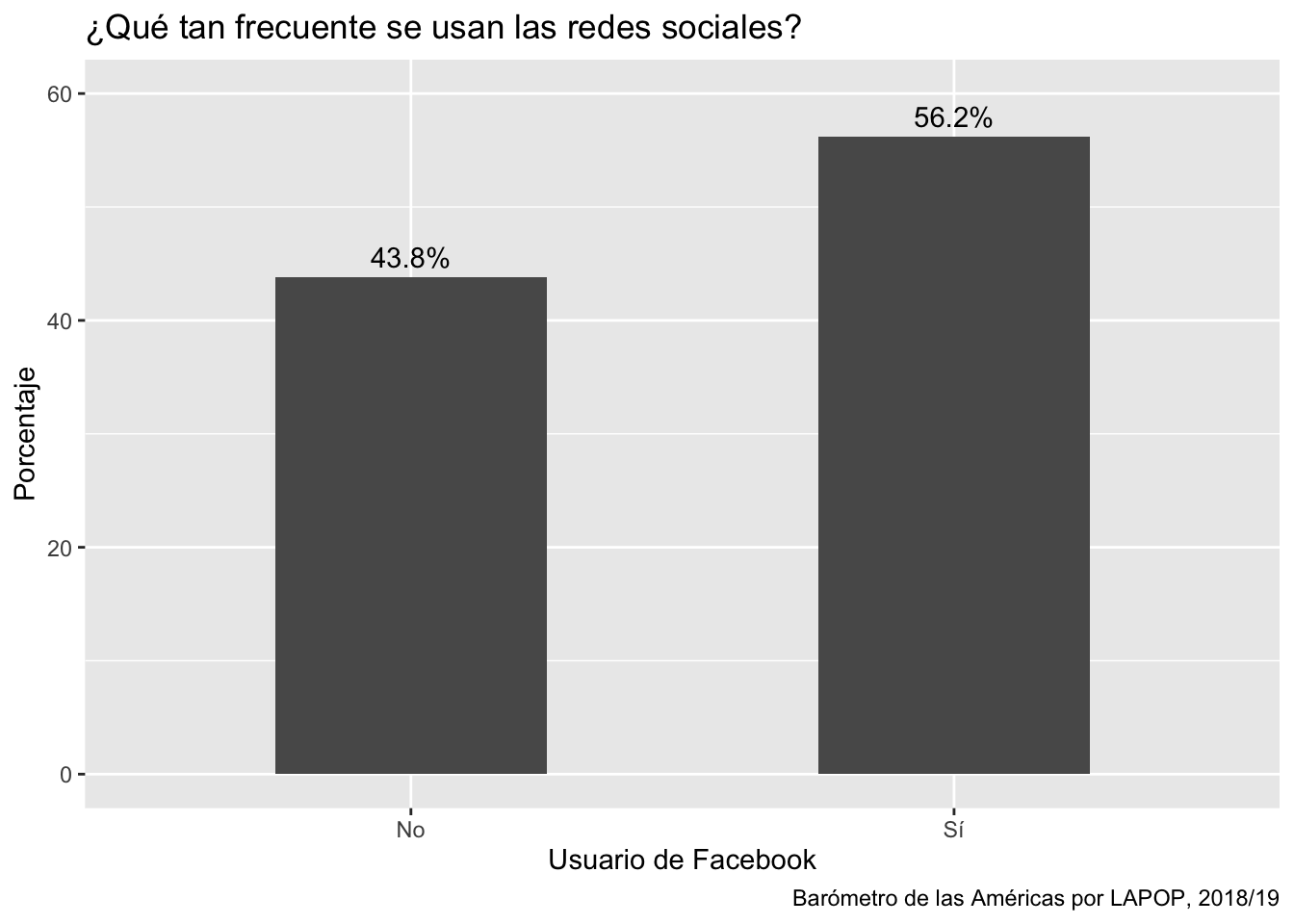

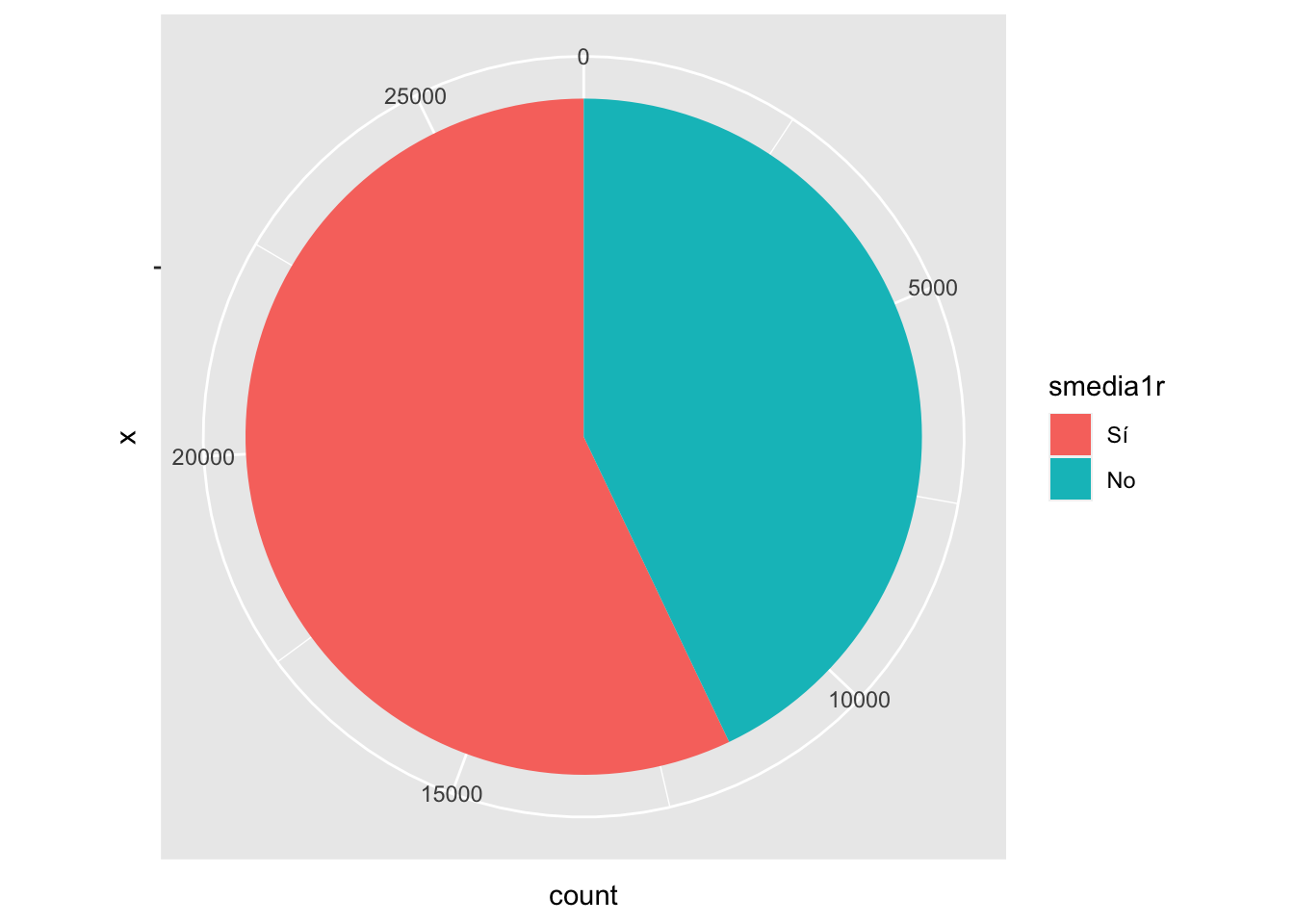
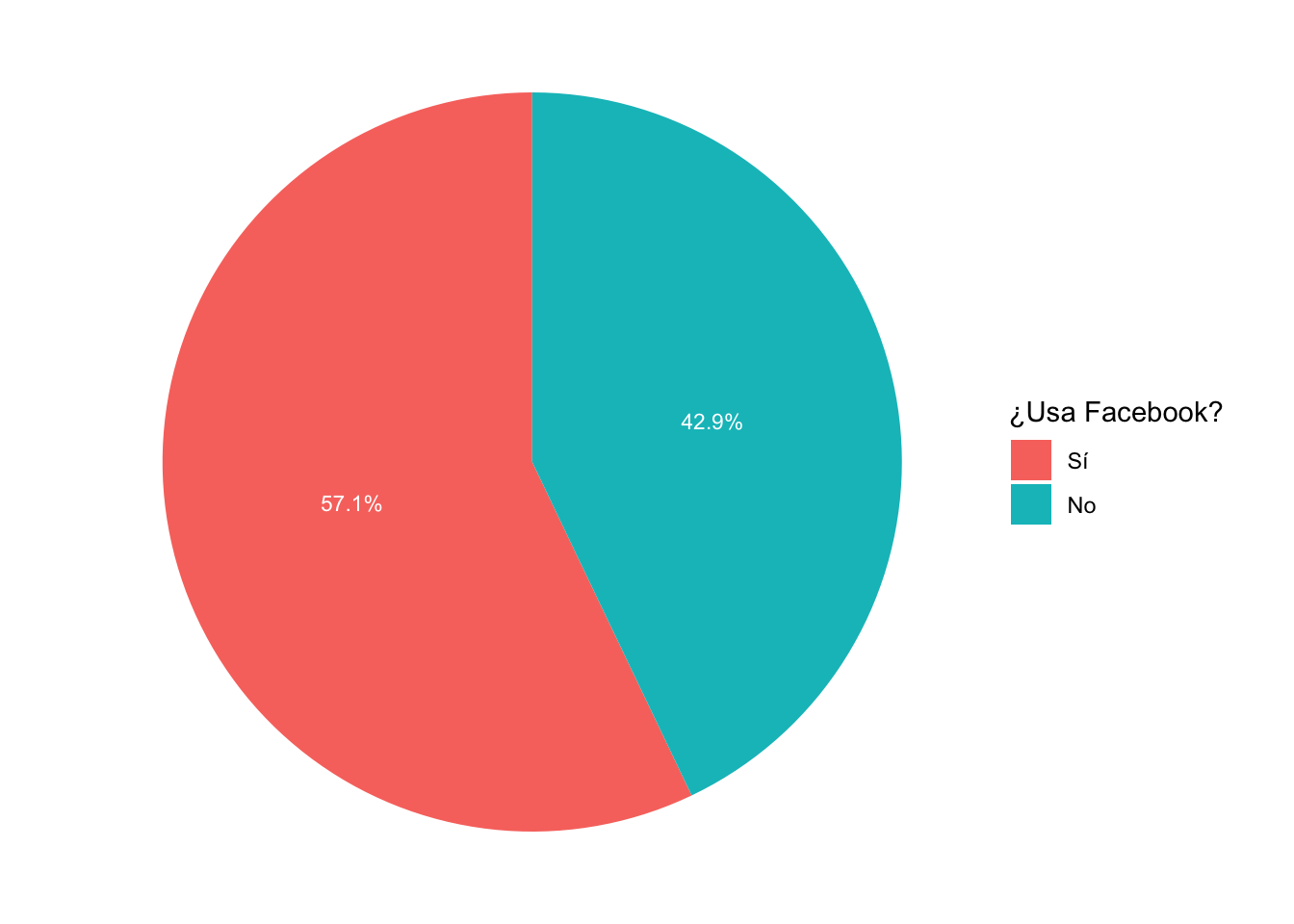
Esto mismo se puede hacer para crear un gráfico circular. Este gráfico reproduce los resultados hallados en el Gráfico 3.1 del reporte.

ggplot(data=fb, aes(x=2, y=per, fill=lab))+
  geom_bar(stat="identity")+
  geom_text(aes(label=paste(round(per, 1), "%", sep="")), color="white", 
            position=position_stack(vjust=0.5), size=3)+
  coord_polar("y")+
  theme_void()+
  labs(title="¿Qué tan frecuente se usan las redes sociales?", 
       caption="Barómetro de las Américas por LAPOP, 2018/19")+
  scale_fill_discrete(name="¿Usa Facebook?")+
  xlim(0.5, 2.5)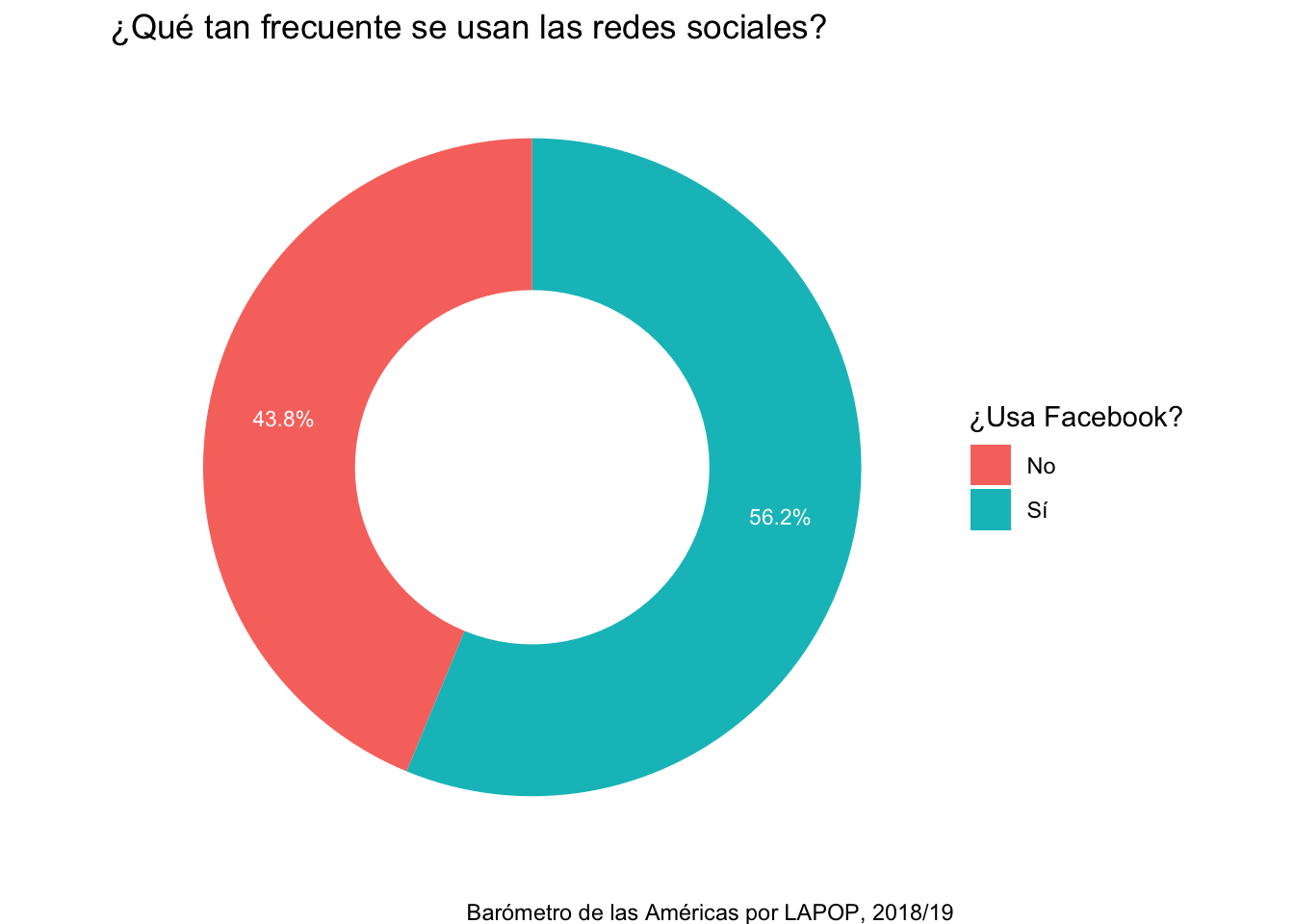

La segunda opción para reproducir los datos del reporte exactamente es mediante el paquete survey. Como se indicó en esta sección, primero se tiene que definir el diseño muestral con el comando svydesign.

library(survey)
diseno18<-svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, nest=TRUE, data=lapop18)

Una vez creado los datos con el factor de expansión en el objeto “lapop.design”, se puede usar los comandos nativos del paquete survey para realizar cálculos. Por ejemplo, para calcular la tabla de distribución de frecuencias se puede usar el comando svytable.

svytable(~fb_user, design=diseno18)

## fb_user
##        0        1 
## 11336.69 14563.60

Estas frecuencias se pueden anidar en el comando prop.table para calcular los porcentajes de usuarios de redes sociales. Estos resultados son iguales a los mostrados en los gráficos anteriores y a los que aparecen en el reporte.

Estos datos también se pueden guardar en un dataframe que se adapta para graficar, siguiendo el mismo procedimiento que en los gráficos anteriores.

prop.table(svytable(~fb_user, design=diseno18))

## fb_user
##         0         1 
## 0.4377052 0.5622948

prop.table(svytable(~tw_user, design=diseno18))

## tw_user
##          0          1 
## 0.92023002 0.07976998

prop.table(svytable(~wa_user, design=diseno18))

## wa_user
##         0         1 
## 0.3563091 0.6436909