Estadística descriptiva usando el Barómetro de las Américas (3)

Introducción

En este documento veremos aspectos básicos de cómo describir una variable numérica. Para eso, vamos a seguir usando el último informe regional “El pulso de la democracia”, disponible aquí, donde se presentan los principales hallazgos de la ronda 2018/19 del Barómetro de las Américas. Una de las secciones de este informe, reporta los datos sobre redes sociales y actitudes políticas. En esta sección, se presentan datos sobre el uso de internet y el uso de redes sociales, en general, por país y por ciertas características sociodemográficas.

Sobre la base de datos

Los datos que vamos a usar deben citarse de la siguiente manera: Fuente: Barómetro de las Américas por el Proyecto de Opinión Pública de América Latina (LAPOP), wwww.LapopSurveys.org. En este documento se carga una base de datos recortada. Esta base de datos se encuentra alojada en el repositorio “materials_edu” de la cuenta de LAPOP en GitHub. Se recomienda limpiar el Environment antes de comenzar este módulo.

Mediante la librería rio y el comando import se puede importar esta base de datos desde este repositorio. Además, se seleccionan los datos de países con códigos menores o iguales a 35, es decir, se elimina las observaciones de Estados Unidos y Canadá.

library(rio)
lapop18 <- import("https://raw.github.com/lapop-central/materials_edu/main/LAPOP_AB_Merge_2018_v1.0.sav")
lapop18 <- subset(lapop18, pais<=35)

Descriptivos para una variable numérica

En la tabla 3.2 del reporte “El pulso de la democracia” se presentan los promedios generales de las variables edad (“q2” en la base de datos) y años de estudio (“ed” en la base de datos) para la población general.

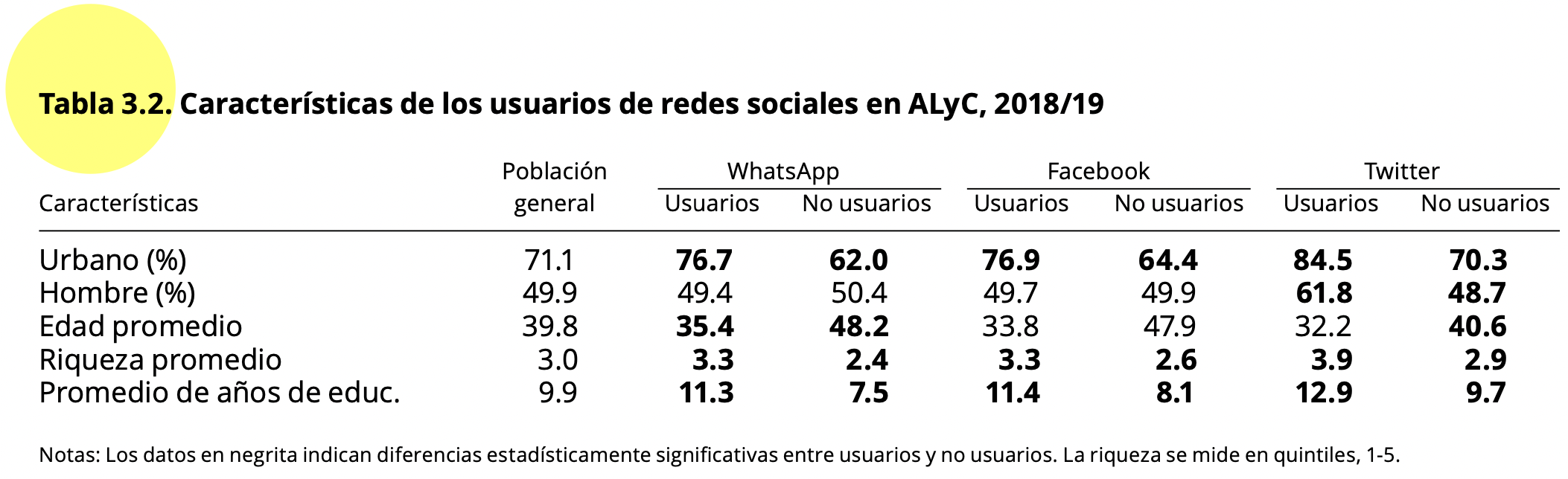
Se usa el comando mean para calcular el promedio y se usa na.rm=T debido a que estas variables cuentan con valores perdidos.

mean(lapop18$q2, na.rm=T)

## [1] 39.99204

mean(lapop18$ed, na.rm=T)

## [1] 9.934748

En la sección donde trabajamos con variables cualitativas (o de factor, en el lenguaje de R), vimos que se podía describir las variables “hombre” y “urbano” definiendo estas variables como factor, etiquetándolas y haciendo una tabla de frecuencias de estas variables. Otra manera de encontrar el porcentaje de personas que son hombres o que viven en el área urbana es trabajar con estas variables, pero no definirlas como factor. Cuando se crean las variables, ambas son definidas por defecto como numéricas. En este caso, además se ser numéricas, son variables de tipo dummy, es decir con valores 0 y 1. En el caso de la variable “hombre” se ha definido 0=Mujer y 1=Hombre; y en el caso de la variable “urbano” se ha definido 0=Rural y 1=Urbano. Es una buena práctica nombrar a la variable dummy con un nombre que refiere a la categoría 1. Con variables dummy, cuando se calcula el promedio, el resultado es el mismo que el porcentaje de la categoría 1. Entonces, si se calcula mean(lapop$hombre, na.rm=T), esta operación nos arroja el porcentaje de la categoría 1, es decir de hombres. Se multiplica por 100 para ponerlo en formato de 0 a 100.

lapop18$hombre <- 2-lapop18$q1
lapop18$urban <- 2-lapop18$ur
mean(lapop18$hombre, na.rm=T)*100

## [1] 49.74846

mean(lapop18$urban, na.rm=T)*100

## [1] 71.15398

Estos son los datos que se presentan en la primera columna de resultados de la población general, excepto para la variable riqueza (“quintall”) que no está disponible en esta versión recortada de la base de datos.

Gráficos descriptivos

Luego de describir una variable numérica, también puede incluir algunas gráficas básicas, por ejemplo, usando el comando hist se puede producir el histograma de la variable “años de educación” (ed).

hist(lapop18$ed)

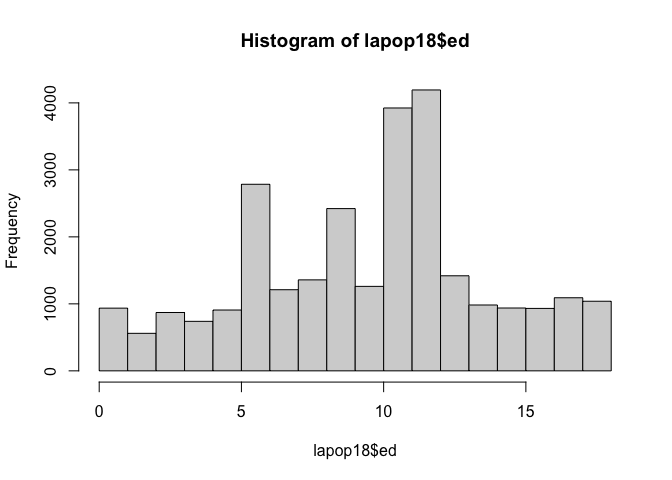
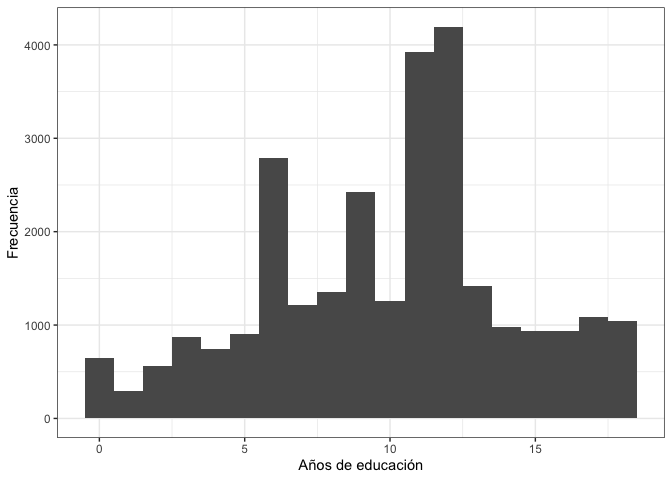
Este mismo gráfico se puede reproducir usando el comando ggplot. Con este comando se tiene más flexibilidad con las opciones gráficas. En primer lugar, se define el dataframe que se usará y la variable “ed” en el eje X. Luego con la especificación geom_histogram() se define usar un histograma. Se define el ancho de la barra del histograma con banwidth=1. Finalmente, este código permite etiquetar el eje X e Y e incluir un tema en blanco y negro, con theme_bw().

library(ggplot2)
ggplot(lapop18, aes(x=ed))+
  geom_histogram(binwidth = 1)+
  xlab("Años de educación")+
  ylab("Frecuencia")+
  theme_bw()

Media por grupos

En la Tabla3.2 del reporte, se presentan la media de estas variables numéricas por grupos de las variables relacionadas a las redes sociales. Es decir, por ejemplo, el promedio de años de estudio para los usuarios de Facebook y para los no usuarios de Facebook. Si queremos calcular el promedio de años de estudio para los usuarios de Facebook, primero se calcula esta variable, de la misma manera que en secciones anteriores, con el comando ifelse.

lapop18$fb_user <- ifelse(lapop18$smedia1==1 & lapop18$smedia2<=4, 1, 0)
lapop18$tw_user <- ifelse(lapop18$smedia4==1 & lapop18$smedia5<=4, 1, 0)
lapop18$wa_user <- ifelse(lapop18$smedia7==1 & lapop18$smedia8<=4, 1, 0)

El cálculo del promedio de años para los usuarios y no usuarios de Facebook se puede hacer de muchas maneras. Una primera es usando los corchetes [...]. En este caso, calcularemos el promedio de años de estudio por grupos de usuarios [lapop18$fb_user==1] y no usuarios de Facebook [lapop18$fb_user==0].

mean(lapop18$ed[lapop18$fb_user==0], na.rm=T)

## [1] 8.064905

mean(lapop18$ed[lapop18$fb_user==1], na.rm=T)

## [1] 11.44839

Descriptivos de una variable numérica por grupos

Otra manera de describir una variable numérica es usando el comando summary. Este comando reporta los estadísticos descriptivos más usados para una variable numérica: mínimo, máximo, cuartiles, media y mediana. Todos estos estadísticos permiten una comparación mejor entre ambos grupos, de usuarios y no usuarios de Facebook. Dentro de este comando se puede incluir la especificación digits=3 para redondear los resultados, lo que evita tener que usar round, por ejemplo.

summary(lapop18$ed[lapop18$fb_user==0], na.rm=T, digits=3)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##    0.00    5.00    8.00    8.06   11.00   18.00    1374

summary(lapop18$ed[lapop18$fb_user==1], na.rm=T, digits=3)

##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.    NA's 
##     0.0     9.0    12.0    11.4    14.0    18.0    1240

Sin embargo, el comando summary no brinda un estadístico importante como la desviación estándar, una medida de dispersión o heterogeneidad. Para poder tener los estadísticos anteriores y que se incluya la desviación estándar, entre otras medidas adicionales, se puede usar el comando describeBy, que es parte de la librería psych. Este comando pide la variable a describir (“ed”) y la variable que forma los grupos (“fb_user”) y brinda la media, la desviación estándar, la mediana, la media recortada, la desviación absoluta de la mediana, el mínimo y máximo.

library(psych)
describeBy(lapop18$ed, lapop18$fb_user)

## 
##  Descriptive statistics by group 
## group: 0
##    vars     n mean  sd median trimmed  mad min max range skew kurtosis   se
## X1    1 11540 8.06 4.3      8    7.99 4.45   0  18    18 0.13    -0.52 0.04
## ------------------------------------------------------------ 
## group: 1
##    vars     n  mean   sd median trimmed  mad min max range  skew kurtosis   se
## X1    1 14998 11.45 3.59     12   11.52 2.97   0  18    18 -0.24        0 0.03

Esta misma información se puede obtener usando el modo de códigos del tidyverse (con el operador pype %>%) y se puede guardar en una tabla. Esta tabla puede guardar los datos de la edad promedio para los usuarios y no usuarios de Whatsapp y además la desviación estándar de cada grupo. En primer lugar definimos con qué dataframe se trabaja. Luego, se indica que no se usen internamente los valores perdidos de la variable usuarios de Whatsapp con filter(!is.na(wa_user)). A continuación se indica que se va a trabajar en grupos de la variable usuarios de Whatsapp con group_by(wa_user). Finalmente, se indica que en cada grupo se calculará la media y la desviación estándar, con summarise.

library(dplyr)
whatxedad <- lapop18 %>%
  filter(!is.na(wa_user)) %>%
  group_by(wa_user) %>%
  summarise(promedio = mean(q2, na.rm=T), sd = sd(q2, na.rm=T))
whatxedad

Gráficos descriptivos por grupos

El reporte no lo muestra, pero se pueden presentar gráficos para cada grupo para facilitar la comparación de una variable. Para hacer estos gráficos comparativos por grupo, vamos a seguir usando el tidyverse. Igual que en la tabla anterior, se define el dataframe y se indica que no se tome en cuenta los valores perdidos de la variable “wa_user”. Luego, se indica que se haga un gráfico, con ggplot que tenga la variable “q2” en el eje X. Se define que este gráfico sea un histograma con geom_histogram(). Una novedad es que, con la especificación facet_wrap(~wa_user) se puede indicar que se hagan gráficos por cada grupo de esa variable. Finalmente, se etiquetan los ejes.

lapop18 %>%
  filter(!is.na(wa_user)) %>%
  ggplot(aes(x=q2))+
  geom_histogram()+
  facet_wrap(~wa_user)+
  xlab("Edad")+
  ylab("Frecuencia")

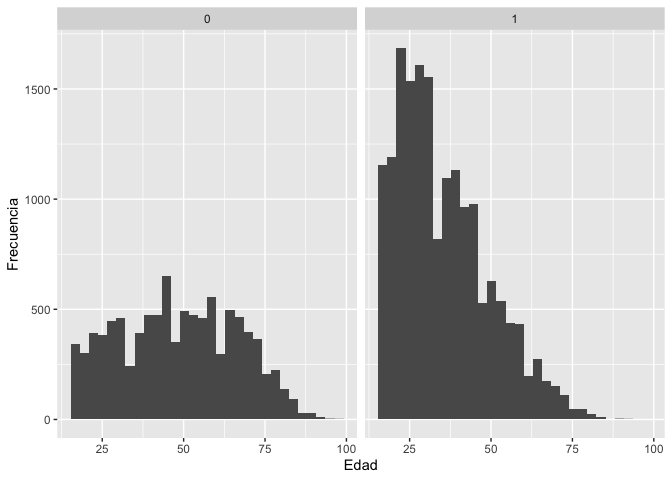
Este gráfico, sin embargo, muestra los valores 0 y 1 de la variable “wa_user” en el encabezado de ambos gráficos. Esto es debido a que esta variable, cuando se creó, se definió por defecto como numérica. Para que aparezcan las etiquetas de la variable, se tiene que transformar “wa_user” en factor y etiquetarla.

lapop18$wa_user = as.factor(lapop18$wa_user)
levels(lapop18$wa_user) <- c("No usuario", "Usuario")

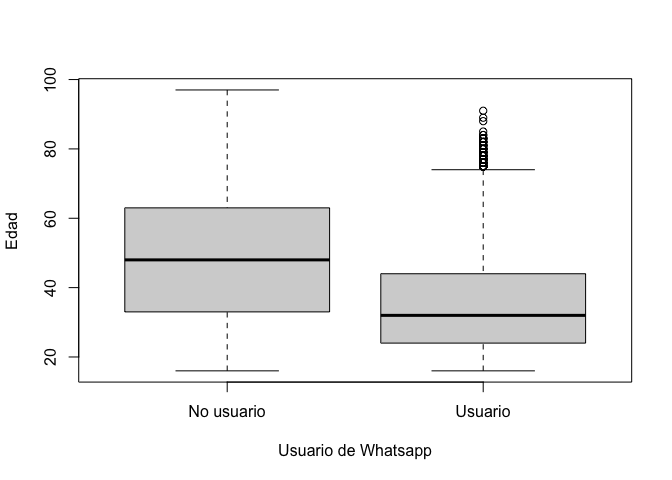
Otra forma de comparar la distribución de edad por grupos de usuarios o no usuarios de Whatsapp es mediante un gráfico de cajas o boxplot. Con el comando boxplot se puede hacer estos gráficos. El comando pide primero la variable en el eje Y, luego la variable que define los grupos y el dataframe. Se puede etiquetar el eje X y Y con los nombres de las variables. Como la variable “wa_user” ha sido transformada a factor y etiquetada, ahora aparecen las etiquetas.

boxplot(q2 ~ wa_user, data=lapop18, xlab ="Usuario de Whatsapp", ylab="Edad")

Resumen

En este documento se ha trabajado con variables numéricas, como edad o años de estudio. Se ha calculado estadísticos descriptivos, como la media o la desviación estándar para toda la población o por grupos. Finalmente, se ha presentado formas de graficar estas variables, mediante histogramas o boxplots.

Cálculos incluyendo el efecto de diseño

Los resultados anteriores no incluyen el factor de expansión. Para incluirlo en los cálculos se puede usar el comando weighted.mean, que es parte de la librería stats, que viene precargada con R, por lo que no hay que instalarla.

weighted.mean(lapop18$q2, lapop18$weight1500, na.rm=T)

## [1] 39.98095

weighted.mean(lapop18$ed, lapop18$weight1500, na.rm=T)

## [1] 9.931417

weighted.mean(lapop18$hombre, lapop18$weight1500, na.rm=T)*100

## [1] 49.74826

weighted.mean(lapop18$urban, lapop18$weight1500, na.rm=T)*100

## [1] 71.11895

Otra forma de calcular la media incluyendo el factor de expansión es mediante de el uso de la librería survey y el comando nativo svymean. Para esto se tiene que definir el diseño muestral con el comando svydesign y guardar este diseño en un objeto, aquí llamado “lapop.design”.

library(survey)
diseno18 <-svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, nest=TRUE, data=lapop18)

Para calcular el promedio, se usa el comando svymean y se usa la especificación na.rm=T debido a que estas variables cuentan con valores perdidos.

svymean(~q2, diseno18, na.rm=T)

##      mean     SE
## q2 39.981 0.0535

svymean(~ed, diseno18, na.rm=T)

##      mean   SE
## ed 9.9314 0.04

Para las variables dummies el procedimiento es el mismo, salvo que se le multiplica por 100 para presentarlo en formato de porcentaje

svymean(~hombre, diseno18, na.rm =T)*100

##          mean    SE
## hombre 49.748 8e-04

svymean(~urban, diseno18, na.rm=T)*100

##         mean     SE
## urban 71.119 0.0076

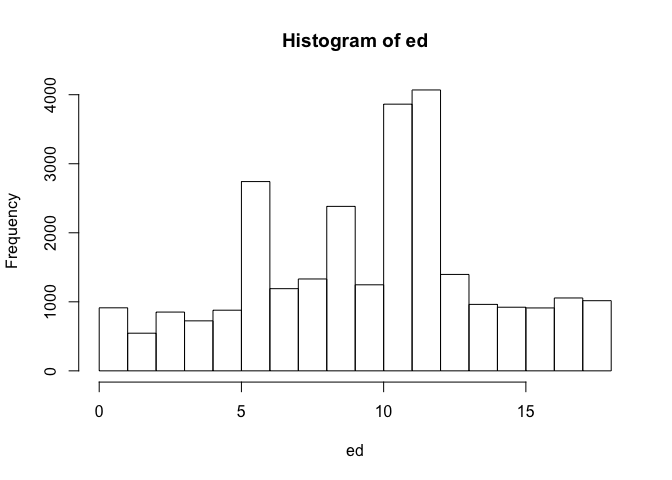
El paquete survey también tiene comandos para replicar gráficos. Por ejemplo, para calcular un histograma simple.

svyhist(~ed, diseno18, freq = T)

Para calcular estadísticos descriptivos por grupos, se puede usar el comando svyby, que permite definir la variable numérica que se quiere describir, la variable que define los grupos y el estadístico ponderado que se quiere calcular.

svyby(~ed, ~fb_user, diseno18, svymean, na.rm=T)

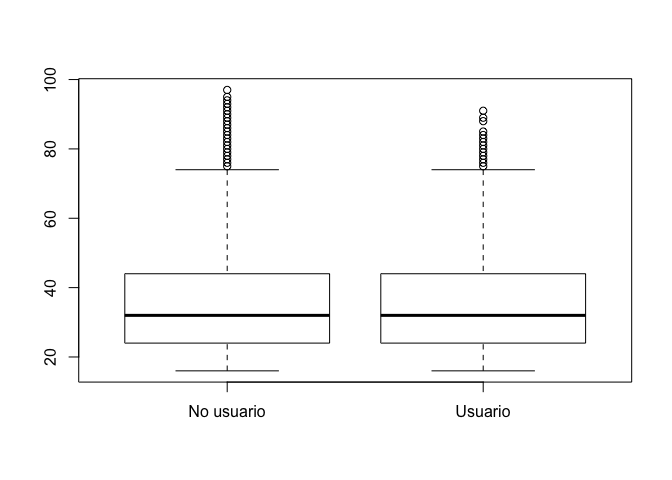
Para reproducir un gráfico descriptivo por grupos, se puede usar el comando svyboxplot para comparar la distribución de la variable edad entre grupos de una variable de tipo factor, como usuarios de Whatsapp.

svyboxplot(~q2~factor(wa_user), diseno18, all.outliers = T)