Manejo de datos usando el Barómetro de las Américas

Introducción

En este documento se verán aspectos básicos del manejo de datos, como la recodificación de una variable, la selección de datos y el cálculo de una nueva variable. Al final se incluye una nota acerca de los cálculos estadísticos considerando el efecto de diseño.

Sobre la base de datos

Los datos que vamos a usar deben citarse de la siguiente manera: Fuente: Barómetro de las Américas por el Proyecto de Opinión Pública de América Latina (LAPOP), wwww.LapopSurveys.org.

En este documento se carga una base que se encuentra alojada en el repositorio “materials_edu” de la cuenta de LAPOP en GitHub. Mediante la librería rio y el comando import se puede importar esta base de datos desde este repositorio, usando el siguiente código. Se importa la base de datos en un objeto “lapop21”. Esta base de datos tiene extensión .RData y cuando se importa, carga las variables como del tipo double (“dbl”), que es un tipo de variable numérica que acepta decimales, a diferencia del tipo integer, “int”, que solo acepta enteros.

library(rio)
lapop21 = import("lapop21.RData")

En este repositorio también se encuentra la base de datos de la ronda anterior, la que también podemos cargar y llamarla “lapop18”. Es necesario aclarar que esta base de datos, importada desde un archivo SPSS, carga las variables como del tipo numéricas (“num”).

lapop18 <- import("https://raw.github.com/lapop-central/materials_edu/main/LAPOP_AB_Merge_2018_v1.0.sav")

Recodificación de una variable

En esta sección usaremos el reporte “El Pulso de la Democracia”, con los resultados de la última ronda 2021 del Barómetro de las Américas, disponible aquí. Este reporte presenta los resultados acerca del apoyo a la democracia en las Américas. Estos resultados se basan en la variable ING4 de la base de datos. Esta variable está fraseada de la siguiente manera:

ING4. Cambiando de nuevo de tema, puede que la democracia tenga problemas, pero es mejor que cualquier otra forma de gobierno. ¿Hasta qué punto está de acuerdo o en desacuerdo con esta frase?

Esta variable está medida en una escala del 1 a 7, donde 1 significa “muy en desacuerdo” y 7 significa “muy de acuerdo”. Luego, los valores entre 5 a 7 son recodificados como apoyo a la democracia. Para ver la distribución de respuestas a esta variable, se puede usar el comando table.

table(lapop21$ing4)

## 
##     1     2     3     4     5     6     7 
##  5704  2567  4980  8177 13886  8390 16759

De esta manera se calculan las observaciones (frecuencias absolutas) por cada valor de la variable. Para calcular el porcentaje de personas que apoya a la democracia se tiene que recodificar esta variable y crear una nueva. Es decir, la variable original ING4, en una escala de 1-7, se tiene que recodificar en una nueva variable, siguiendo la siguiente regla:

1. Valores entre 1-4 de ING4 se transforman en 0 en una nueva variable ing4r
2. Valores entre 5-7 de ING4 se transformen en 1 en una nueva variable ing4r

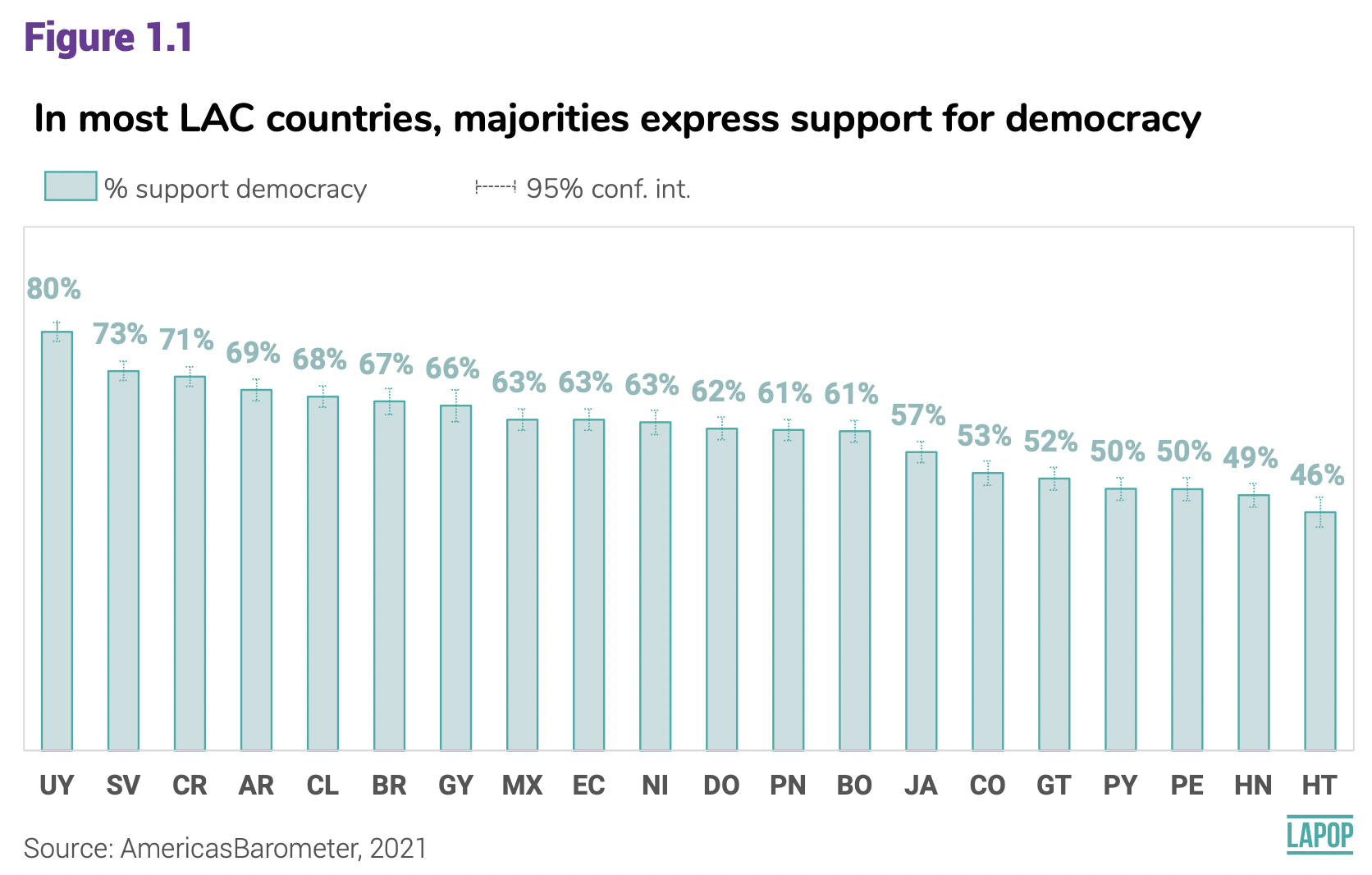
Un ejemplo de cómo se presentan estos datos recodificados en el reporte se puede ver en el Gráfico 1.1. Este muestra el porcentaje de ciudadanos que apoya a la democracia por país. Es decir, se muestra el porcentaje de entrevistados que respondieron entre 5 y 7 a la pregunta ING4 en cada país. De acuerdo a la recodificación planteada, este gráfico representaría el porcentaje de entrevistados que registra un 1 en la variable recodificada.

En el informe El Pulso de la Democracia de la ronda 2018/19, disponible aquí, también se presenta un gráfico similar, usando la misma variable y la misma regla de recodificacíon.

Para recodificar una variable en R hay varias formas. Una de las formas más eficientes de hacerlo es usando el comando recode del paquete car. El paquete dplyr tiene un comando recode que puede confundir a R. Para evitar confusiones usaremos la sintaxis car::recode para la recodificación, es decir para especificar que se use el comando recodedel paquete car y no de otro. Se guarda la variable recodificada como “lapop21$ing4rec”. Luego, se usa el comando table para describir esta nueva variable.

library(car)
lapop21$ing4rec <- car::recode(lapop21$ing4, "1:4=0; 5:7=1")
table(lapop21$ing4rec)

## 
##     0     1 
## 21428 39035

Si se suman las observaciones entre 1 y 4 de la variable original (5704+2567+4980+8177), vemos que es el resultado que se tiene en el valor 0 de la nueva variable (21428), tal como se escribió en la recodificación. También se debe notar que la base de datos en el Environment ahora tiene una variable más, totalizando 1826 variables.

Selección de casos

El gráfico 1.1 muestra que el apoyo a la democracia va de un máximo de 80% en Uruguay a un mínimo de 46% en Haití. Para replicar el resultado correspondiente a Uruguay se puede seleccionar las observaciones de ese país. De acuerdo a la codificación de la variable “pais”, Uruguay tiene el código 14.

La selección de casos en R se puede hacer de múltiples maneras. Una forma es usar los corchetes \[ \]. Otra forma es usando el comando subset. Con este comando seleccionamos las observaciones de este país y guardamos esta selección en un nuevo dataframe “lapop2” usando este último comando. Se tiene 3009 observaciones en Uruguay.

lapop1 <- subset(lapop21, pais==14)
table(lapop1$pais)

## 
##   14 
## 3009

Con esta selección de datos, se puede calcular el porcentaje (frecuencias relativas) usando el comando prop.table. Este comando nos brinda las frecuencias relativas (en valores entre 0 y 1) de una tabla de frecuencias calculada con table. Estas frecuencias relativas se multiplican por 100 para reproducir el porcentaje en cada país. En este caso se usan los \[ \] para hacer la selección de casos de cada país.

prop.table(table(lapop1$ing4rec[lapop1$pais==14]))*100

## 
##        0        1 
## 15.47499 84.52501

Estos resultados son porcentajes (entre 0 y 100), pero incluyen muchos decimales. Para redondear a un decimal, como se muestra en el Gráfico 1.2, se puede usar el comando round, donde se anida toda la sintaxis anterior. En este comando, además, se tiene que especificar el número de decimales que se quiere, que en este caso es 1.

round(prop.table(table(lapop1$ing4rec[lapop1$pais==14]))*100, 1)

## 
##    0    1 
## 15.5 84.5

Según este resultado 84.5% de uruguayos apoya a la democracia. Este resultado es distinto al que se reporta en el gráfico 1.1, donde el valor reportado es 80%. Esta diferencia es debido a que estos primeros procedimientos no incluyen el efecto de diseño. Más abajo se verá el procedimiento para reproducir el resultado exacto reportado.

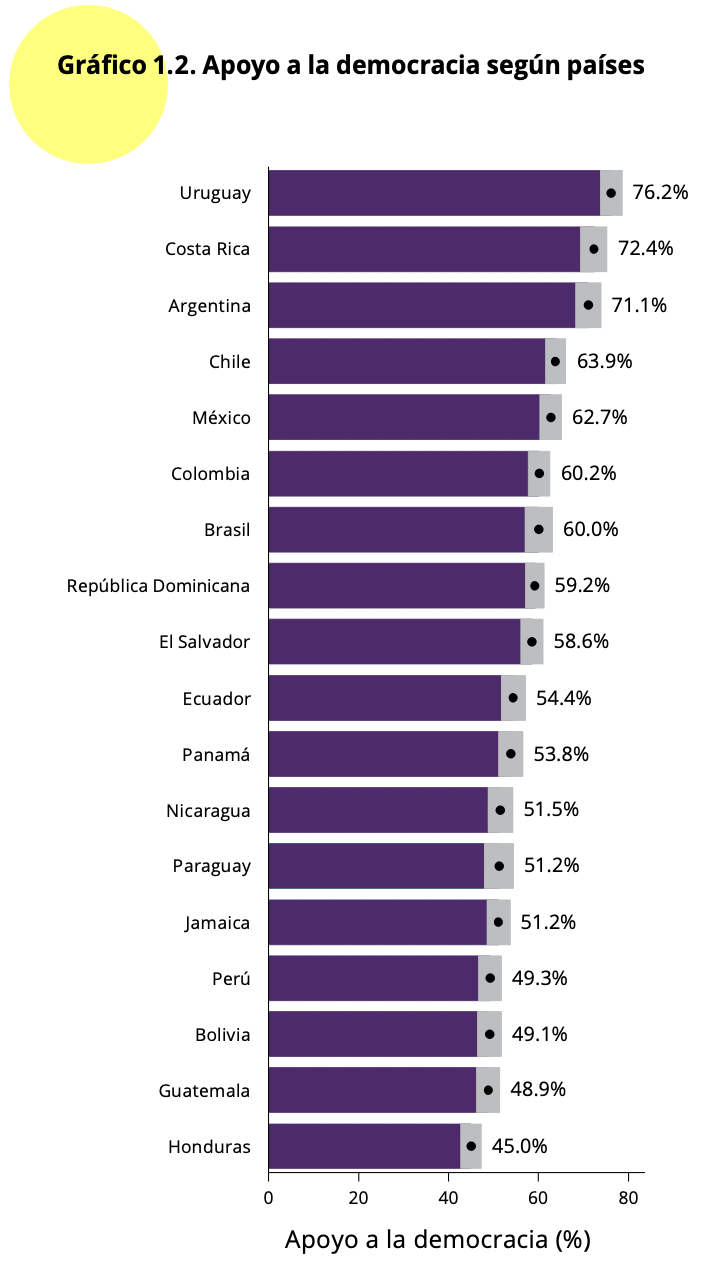
En el reporte de la ronda 2018/19 el reporte indica que “El Gráfico 1.2 muestra el porcentaje de personas en cada país que expresa apoyar la democracia en 2018/19. El apoyo a la democracia va de un mínimo de 45% en Honduras a un máximo de 76.2% en Uruguay” (p.11).

Para replicar estos resultados acerca de Honduras y acerca de Uruguay para 2018/19, se podría seleccionar los datos de estos dos países. De acuerdo al cuestionario, que se puede ver aquí, Honduras es el país 4 y Uruguay es el país 14 de la variable “pais”, que también se ha importando como una variable numérica.

Se incluye el operador “o”, que en R se denota con “|”. De esta manera se indica que se selecciones las observaciones de Honduras o de Uruguay (pais==4 | pais==14). La descripción de la variable “pais” muestra que solo incluye los casos de Honduras (2) y Uruguay (14).

# lapop2 <- lapop18[lapop18$pais == 4 | lapop18$pais==14, ]
lapop2 <- subset(lapop18, pais==4 | pais==14)
table(lapop2$pais)

## 
##    4   14 
## 1560 1581

El nuevo dataframe “lapop2” tiene 3141 observaciones y 84 variables debido a que no se ha creado la variable recodificada.

lapop2$ing4rec <- car::recode(lapop2$ing4, "1:4=0; 5:7=1")

Con esta variable se pueden seguir los mismos procedimientos anteriormente descritos: producir la tabla de frecuencias relativas.

prop.table(table(lapop2$ing4rec[lapop2$pais==4]))*100

## 
##        0        1 
## 54.98995 45.01005

prop.table(table(lapop2$ing4rec[lapop2$pais==14]))*100

## 
##        0        1 
## 23.80641 76.19359

Y luego incluir el redondeo.

round(prop.table(table(lapop2$ing4rec[lapop2$pais==4]))*100, 1)

## 
##  0  1 
## 55 45

round(prop.table(table(lapop2$ing4rec[lapop2$pais==14]))*100, 1)

## 
##    0    1 
## 23.8 76.2

Con este código se ha reproducido los resultados de los países en los extremos del Gráfico 1.2 del reporte. En este caso, los resultados sí son similares a los reportados en el gráfico.

Ambos reportes también indican que se excluye de los cálculos a Estados Unidos y Canadá. La base de datos cargada como “lapop18” incluye a todos los países de la ronda. Para excluir a estos dos países, se tiene que seleccionar los países que NO son EE.UU. y Canadá. Esta nueva selección se puede guardar en un nuevo dataframe o se puede sobreescribir en el dataframe original, como se hace en este caso debido a que la exclusión de estos países es para todos los cálculos que siguen. De acuerdo al cuestionario, EE.UU. tiene el código 40 y Canadá, el código 41 en la variable “pais”. Para excluirlos se tiene que incluir a los países que tengan un código menor a 40 (o de 35 o menos). Para esto nuevamente podemos usar el comando subset.

lapop18 <- subset(lapop18, pais<=35)

Se puede observar en el Environment que se reducen las observaciones del dataframe “lapop18” luego de correr este código, pues se han eliminado las observaciones de entrevistados en estos dos países. El número de observaciones pasa de 31,050 a 28,042, número que coincide con el de la base de datos en formato .RData que usamos en el módulo anterior y que indicamos que no incluía a estos países.

De la misma manera se puede proceder en la base de datos de la ronda 2021, con lo que disminuyen las observaciones a 60661.

lapop21 <- subset(lapop21, pais<=35)

Calcular una variable

Una práctica frecuente de LAPOP con los datos del Barómetro de las Américas es el re-escalamiento de variables. El capítulo sobre legitimidad democrática del reporte brinda ejemplos de este re-escalamiento con variables relacionadas al apoyo al sistema. Para calcular este índice de apoyo al sistema se trabaja con un conjunto de cinco variables:

B1. ¿Hasta qué punto cree usted que los tribunales de justicia de (país) garantizan un juicio justo? \[Sondee: Si usted cree que los tribunales no garantizan para nada la justicia escoja el número 1; si cree que los tribunales garantizan mucho la justicia, escoja el número 7 o escoja un puntaje intermedio\].

B2. ¿Hasta qué punto tiene usted respeto por las instituciones políticas de (país)?

B3. ¿Hasta qué punto cree usted que los derechos básicos del ciudadano están bien protegidos por el sistema político de (país)?

B4. ¿Hasta qué punto se siente orgulloso de vivir bajo el sistema político de (país)?

B6. ¿Hasta qué punto piensa usted que se debe apoyar al sistema político de (país)?

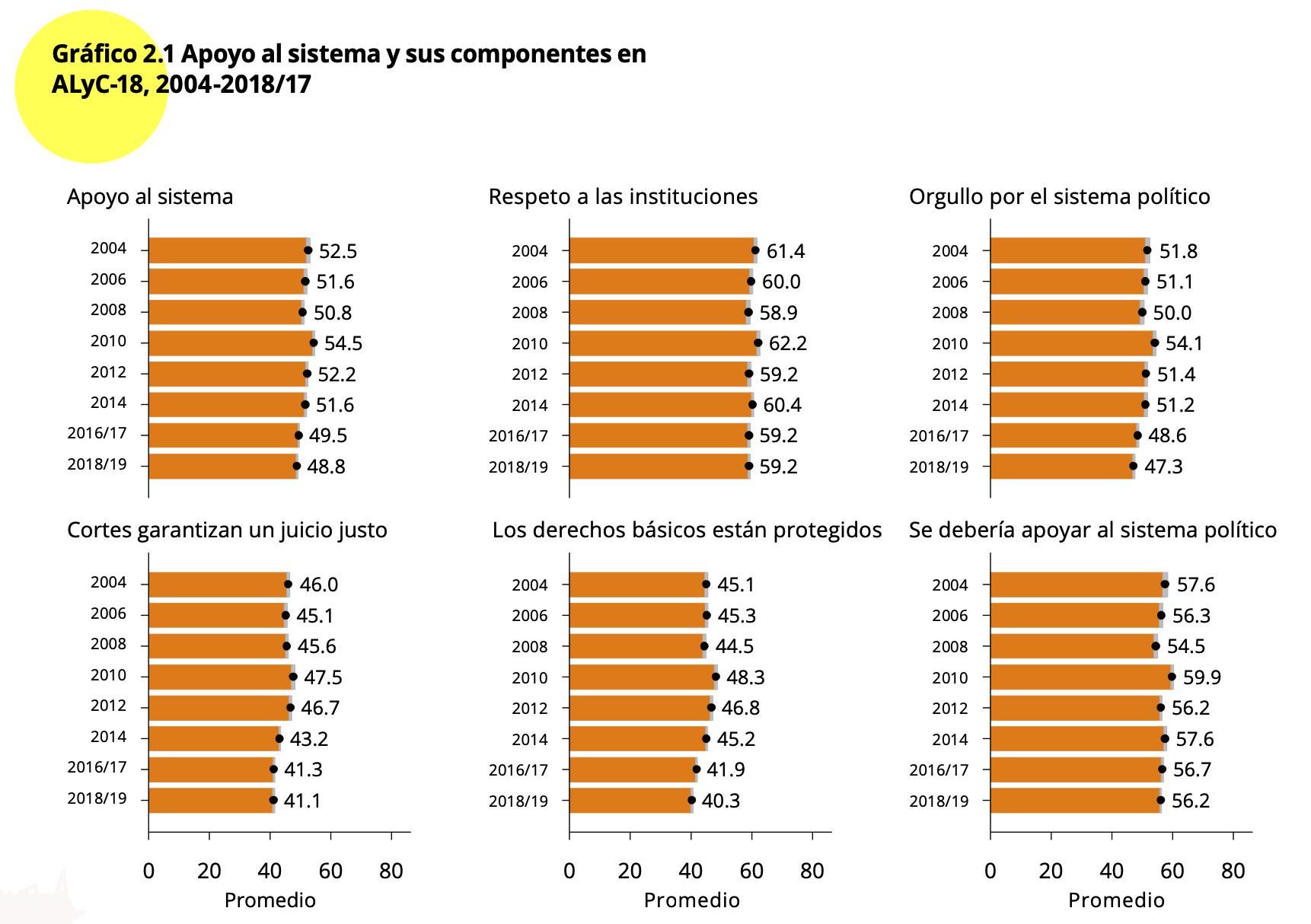
Como indica el reporte “Para cada pregunta, la escala original de 1 (”Nada”) a 7 (“Mucho”) se recodifica en una escala de 0 a 100, de tal forma que 0 indica el menor nivel de apoyo al sistema político y 100 es el nivel máximo de apoyo al sistema político. Esta nueva escala sigue la recodificación típica de LAPOP y puede ser interpretada como una medición del apoyo en unidades, o grados, en una escala continua que va de 0 a 100” (p.34). Para comprobar la escala original de estas variables, se puede describir estas variables usando el comando table.

table(lapop18$b1)

## 
##    1    2    3    4    5    6    7 
## 4089 4067 5881 6137 4215 1631 1371

table(lapop18$b2)

## 
##    1    2    3    4    5    6    7 
## 2861 2152 2998 4153 5182 4448 5679

table(lapop18$b3)

## 
##    1    2    3    4    5    6    7 
## 5080 4096 5153 5349 4219 2061 1491

table(lapop18$b4)

## 
##    1    2    3    4    5    6    7 
## 5095 3206 3743 4557 4326 3041 3584

table(lapop18$b6)

## 
##    1    2    3    4    5    6    7 
## 3713 2325 2971 4277 4616 3868 5572

Se observa que efectivamente todas las variables corren en una escala de 1 a 7. Para reescalar una variable en una escala original de 1 a 7 a otra de 0 a 100, lo primero que se tiene que hacer es restar 1 unidad, con lo que la variable tendría una escala de 0 a 6, luego dividirla entre 6, con lo que variaría entre 0 y 1 y, finalmente, multiplicarla por 100. Esto es:

Variable reescalada = ((variable original -1)/6)*100

lapop18$b1rec <- ((lapop18$b1-1)/6)*100
lapop18$b2rec <- ((lapop18$b2-1)/6)*100
lapop18$b3rec <- ((lapop18$b3-1)/6)*100
lapop18$b4rec <- ((lapop18$b4-1)/6)*100
lapop18$b6rec <- ((lapop18$b6-1)/6)*100
table(lapop18$b1rec)

## 
##                0 16.6666666666667 33.3333333333333               50 
##             4089             4067             5881             6137 
## 66.6666666666667 83.3333333333333              100 
##             4215             1631             1371

Con esta transformación se observa que los 4,089 entrevistados que marcaron 1 en la pregunta B1, ahora tienen un puntaje de 0. Los 4,067 que marcaron 2, ahora tienen un puntaje de 16.67, es decir 2-1=1/6=0.1667*100=16.67. Esta misma operación se pudo hacer con el comando car::recode, siguiendo la siguiente regla de recodificación:

• Valor de 1 en variable original se recodifica como 0 en nueva variable
• Valor de 2 en variable original se recodifica como 16.67 en nueva variable
• Valor de 3 en variable original se recodifica como 33.33 en nueva variable
• Valor de 4 en variable original se recodifica como 50 en nueva variable
• Valor de 5 en variable original se recodifica como 66.67 en nueva variable
• Valor de 6 en variable original se recodifica como 83.33 en nueva variable
• Valor de 7 en variable original se recodifica como 100 en nueva variable

Esta manera de recodificar, sin embargo, es poco eficiente. Es más simple usar la fórmula para calcular la recodificación.

Para calcular el índice de apoyo al sistema, el reporte indica que “El índice de apoyo al sistema es el promedio de cinco preguntas: B1, B2, B3, B4 y B6” (p.46). Es decir, con las variables reescaladas se tiene que calcular el promedio de estas cinco variables para cada individuo (es decir, en cada fila de la base de datos). Esta operación se podría realizar calculando el promedio de forma manual.

Apoyo al sistema = (b1rec + b2rec + b3rec + b4rec + b6rec)/5

En R tenemos el comando rowMeans que sirva para calcular promedios de ciertas columnas por cada fila. La sintaxis [, 86:90] indica que se realizará el cálculo del promedio por filas para todas las filas y usando las columnas 86 a 90 del dataframe “lapop18” (se podría hacer el cálculo para algunas filas en particular definiendo [fila_n:fila_m, 86:90]). Este promedio se guarda en una nueva variable “apoyo”, que se describe.

lapop18$apoyo <- rowMeans(lapop18[,86:90])
table(lapop18$apoyo)

## 
##                0 3.33333333333333 6.66666666666667               10 
##              634              368              439              525 
## 13.3333333333333 16.6666666666667               20 23.3333333333333 
##              527              550              834              745 
## 26.6666666666667               30 33.3333333333333 36.6666666666667 
##              810              911             1063             1086 
##               40 43.3333333333333 46.6666666666667               50 
##             1287             1317             1254             1487 
## 53.3333333333333 56.6666666666667               60 63.3333333333333 
##             1397             1408             1449             1243 
## 66.6666666666667               70 73.3333333333333 76.6666666666667 
##             1227             1113              988              827 
##               80 83.3333333333333 86.6666666666667               90 
##              820              572              445              369 
## 93.3333333333333 96.6666666666667              100 
##              245              131              210

Con este índice se puede calcular el apoyo al sistema promedio para la última ronda del Barómetro de las Américas, así como los promedios de cada una de las variables que componen el índice. Se usa el comando mean para el promedio y la especificación na.rm=T para indicarle al comando que no tome en cuenta los valores perdidos de estas variables. Estos estadísticos se verán en más detalle en otros documentos.

mean(lapop18$apoyo, na.rm=T)

## [1] 48.79419

mean(lapop18$b1rec, na.rm=T) #Cortes garantizan juicio justo

## [1] 41.06032

mean(lapop18$b2rec, na.rm=T) #Respeto a las instituciones

## [1] 59.23937

mean(lapop18$b3rec, na.rm=T) #Derechos básicos están protegidos

## [1] 40.42406

mean(lapop18$b4rec, na.rm=T) #Orgullos por el sistema político

## [1] 47.41096

mean(lapop18$b6rec, na.rm=T) #Se debería apoyar al sistema político

## [1] 56.28337

Estos resultados son los que se muestran en el Gráfico 2.1 para la ronda 2018/19.

Calcular una variable de manera condicional

En algunas ocasiones el cálculo de una variable no requiere solamente la transformación numérica de la variable original, sino que los valores de la nueva variable dependen de valores de otras variables. Por ejemplo, el capítulo “Redes sociales y actitudes políticas” del reporte “El Pulso de la Democracia” presenta los resultados para las variables “usuario de Whatsapp”, “usuario de Twitter” y “usuario de Facebook”. Para calcular estas variables, el pie de página 7 de este capítulo indica: “Para cada plataforma, se identifican los usuarios con una combinación de dos conjuntos de preguntas. Primero, se identifican como usuarios a quienes responden positivamente a las preguntas, SMEDIA1/SMEDIA4/SMEDIA7. ¿Tiene usted cuenta de Facebook/Twitter/Whatsapp? Luego, se recodifica como no usuario a quienes responden”nunca” a las preguntas siguientes, SMEDIA2/SMEDIA5/SMEDIA8. ¿Con qué frecuencia ve contenido en Facebook/Twitter/Whatsapp?” (p. 64).

Es decir, el usuario no solo es el que tiene una cuenta (SMEDIA1=1), sino el que la usa con cierta frecuencia (SMEDIA2=1, 2, 3, 4). De esta manera, el no usuario puede tener una cuenta, pero nunca usarla. Por lo tanto, la variable “usuario” depende de los valores de 2 variables. La regla de codificación que se sigue es:

• Usuario de Facebook = 1 (sí es usuario) si SMEDIA1 = 1 (tiene cuenta) y SMEDIA2 <= 4 (la usa con alguna frecuencia)

• Usuario de Facebook = 0 (no es usuario) si SMEDIA2 = 2 (no tiene cuenta) o SMEDIA2 = 5 (tiene cuenta pero nunca la usa)

Esta regla se transforma en la siguiente sintaxis de R, que usa el comando ìfelse. Esta sintaxis incluye la condición para asignar valores de 1 a una nueva variable y asigna a todas las demás observaciones el valor de 0. Se describen estas nuevas variables usando los comandos table para generar las frecuencias absolutas, prop.table para las frecuencias relativas y round para redondear los decimales. Estos comandos se verán en más detalle en los siguientes documentos.

lapop18$fb_user <- ifelse(lapop18$smedia1==1 & lapop18$smedia2<=4, 1, 0)
lapop18$tw_user <- ifelse(lapop18$smedia4==1 & lapop18$smedia5<=4, 1, 0)
lapop18$wa_user <- ifelse(lapop18$smedia7==1 & lapop18$smedia8<=4, 1, 0)
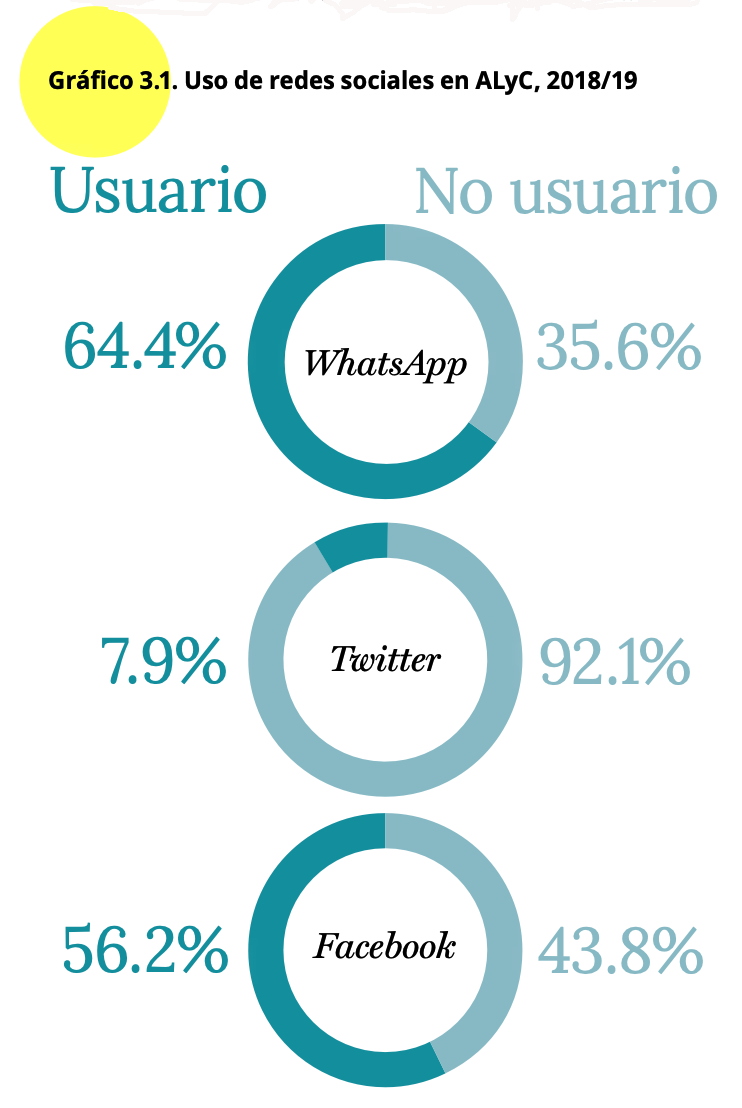
round(prop.table(table(lapop18$fb_user))*100, 1)

## 
##    0    1 
## 43.8 56.2

round(prop.table(table(lapop18$tw_user))*100, 1)

## 
##    0    1 
## 92.1  7.9

round(prop.table(table(lapop18$wa_user))*100, 1)

## 
##    0    1 
## 35.8 64.2

Estos resultados son los que se presentan en el Gráfico 3.1 del reporte en forma de gráficos circulares. Este tipo de gráficos se verán en la sección siguiente.

Observación del efecto de diseño

Tanto los resultados para apoyo al sistema, como los de usuarios de redes sociales difieren de los que aparecen en el reporte por dos motivos. En primer lugar, para apoyo al sistema, debido a que “Los valores a lo largo del tiempo se calculan incluyendo únicamente los países que el Barómetro de las Américas ha estudiado regularmente desde 2006: Argentina, Brasil, Bolivia, Chile, Colombia, Costa Rica, República Dominicana, Ecuador, El Salvador, Guatemala, Honduras, Jamaica, México, Nicaragua, Panamá, Paraguay, Perú, Uruguay” (p.46). El código solo filtra la última ronda, que incluye países que no están en esa lista, como Estados Unidos o Canadá. De otro lado, los cálculos reportados en la publicación incluyen el uso de factores de expansión, que no se han incluido en estos cálculos, pero que en otros documentos se incorporarán (ver aquí).

Resumen

En este documento se han visto los elementos básicos de la manipulación y transformación de datos usando el Barómetro de las Américas. Se ha recodificado una variable usando el comando recode, se ha seleccionado casos usando subset y se ha calculado una nueva variable algebraicamente y con el comando ìfelse.