Introducción
En este documento veremos como comparar dos medias y saber si las
diferencias se pueden inferir a la población, mediante la prueba t de
comparación de medias. Para eso, vamos a seguir usando los últimos
reportes “El pulso de la democracia”, del 2021, disponible aquí,
y del 2018/19, disponible aquí,
donde se presentan los principales hallazgos del Barómetro de las
Américas.
En el reporte 2021 se presentan los resultados sobre la victimización
por el crimen por grupos de género, edad, educación y riqueza (ver
Gráfico 3.12). En el informe de la ronda 2018/19 se reportan los
resultados sobre apoyo a la democracia electoral, variable que se cruza
con algunas otras variables sociodemográficas como sexo o lugar de
residencia (ver Gráfico 1.5).
En esta sección analizaremos los casos cuando la victimización por el
crimen se compara entre hombres y mujeres y cuando el apoyo a la
democracia se compara entre grupos de género y de residencia urbana o
rural.
Sobre la base de datos
Los datos que vamos a usar deben citarse de la siguiente manera:
Fuente: Barómetro de las Américas por el Proyecto de Opinión Pública de
América Latina (LAPOP), wwww.LapopSurveys.org. En este documento se
carga una base de datos recortada. Esta base de datos se encuentra
alojada en el repositorio “materials_edu” de la cuenta de LAPOP en
GitHub. Se recomiendo limpiar el Environment antes de proceder con esta
sección.
Mediante la librería rio y el comando
import se puede importar esta base de datos desde este
repositorio. Además, se seleccionan los datos de países con códigos
menores o iguales a 35, es decir, se elimina las observaciones de
Estados Unidos y Canadá.
library(rio)
lapop18 <- import("https://raw.github.com/lapop-central/materials_edu/main/LAPOP_AB_Merge_2018_v1.0.sav")
lapop18 <- subset(lapop18, pais<=35)
También cargamos la base de datos de la ronda 2021.
lapop21 = import("lapop21.RData")
lapop21 <- subset(lapop21, pais<=35)
Victimización por el crimen
La victimización por el crimen está medida con la variable “vic1ext”.
La pregunta está fraseada: “Ahora, cambiando de tema, ¿ha sido usted
víctima de algún acto de delincuencia en los últimos 12 meses? Es decir,
¿ha sido víctima de un robo, hurto, agresión, fraude, chantaje,
extorsión, amenazas o algún otro tipo de acto delincuencial en los
últimos 12 meses?”.
Esta variable está codificada como 1 “Sí” y 2 “No. Para poder
replicar los resultados del gráfico 3.12 tenemos que recodificar esta
variable. Como indicamos en el módulo anterior, esta codificación nos
permite calcular el porcentaje de víctimas del crimen mediante el
comando mean. El resultado nos indica que el 22% de
ciudadanos en la región reporta haber sido víctima del crimen.
library(car)
lapop21$crimen <- car::recode(lapop21$vic1ext, "1=100; 2=0")
mean(lapop21$crimen, na.rm=T)
## [1] 21.92233
El gráfico 3.12 muestra la comparación de la victimización por el
crimen cruzada por cuatro variables sociodemográficas: género, edad,
educación y quintiles de riqueza.
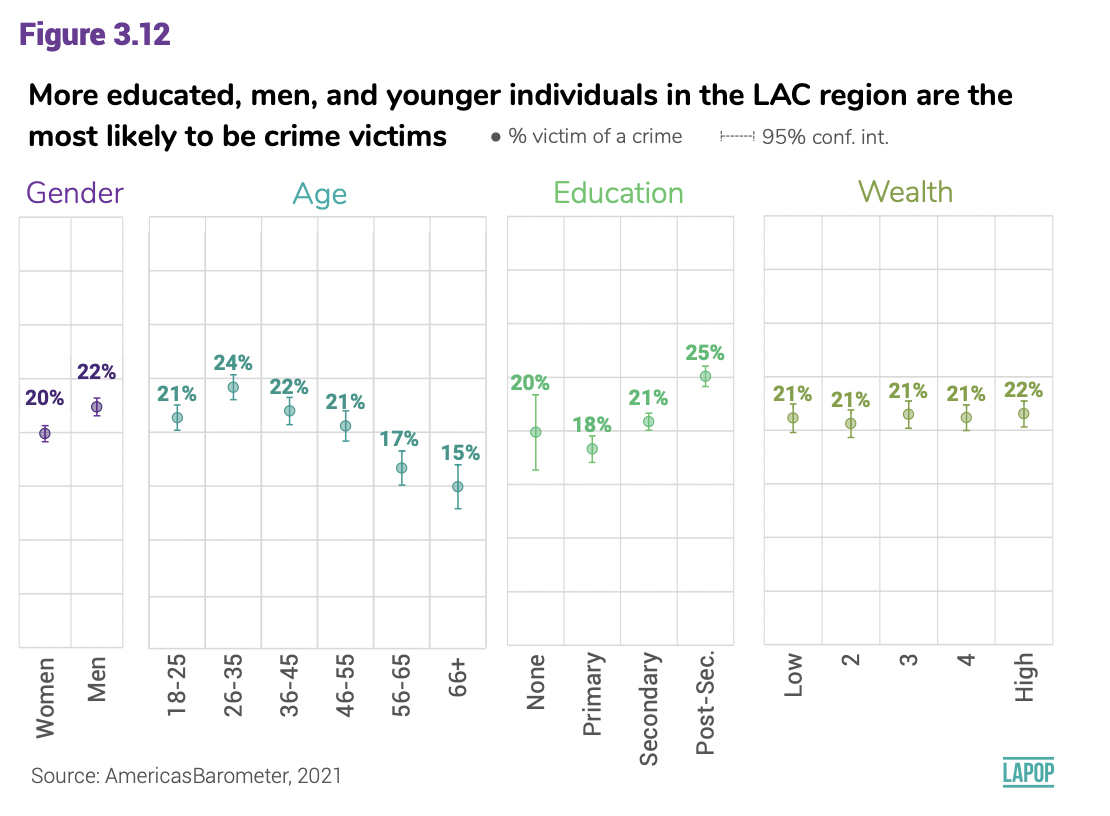
Para replicar las diferencias entre géneros, se tiene que recodificar
la variable “q1tb” y luego declararla como factor.
lapop21$genero = car::recode(lapop21$q1tb, "1=2; 2=1; 3=1")
lapop21$genero = as.factor(lapop21$genero)
levels(lapop21$genero) = c("Mujer", "Hombre")
table(lapop21$genero)
##
## Mujer Hombre
## 31487 29174
De la misma manera que en el documento sobre intervalos de confianza,
usamos el comando tapply para calcular el porcentaje de
victimización por crimen por grupos de género.
tapply(lapop21$crimen, lapop21$genero, mean, na.rm=T) #Para género
## Mujer Hombre
## 20.87127 23.06949
Para reproducir el gráfico de barras, incluyendo los intervalos de
confianza, primero se puede producir una tabla que guarde el valor del
porcentaje de cada grupo, así como el valor inferior y superior del
intervalo de confianza. Esto se puede hacer con el comando
group.CI del paquete Rmisc.
Con esta table, se puede usar la librería ggplot para
reproducir el primer panel del gráfico 3.12. Los resultados no son
idénticos dado que no se ha usado el efecto de diseño.
library(Rmisc)
crxgen <- group.CI(crimen~genero, lapop21)
library(ggplot2)
graf3.12a <- ggplot(crxgen, aes(x=genero, y=crimen.mean))+
geom_bar(width=0.5, fill="darkcyan", colour="black", stat="identity")+
geom_errorbar(aes(ymin=crimen.lower, ymax=crimen.upper), width=0.2)+
geom_text(aes(label=paste(round(crimen.mean, 1), "%")), vjust=-1.5, size=4)+
xlab("Género") + ylab("Victimización por crimen (%)")+
ylim(0, 40)
graf3.12a
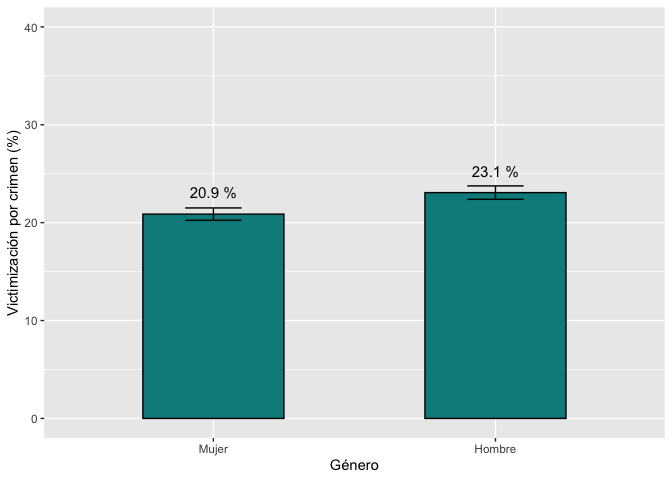
En este gráfico se puede comparar visualmente los intervalos de
confianza de cada grupo. Como estos no se traslapan, se puede concluir
de manera inicial que existen diferencias estadísticamente
significativas entre hombres y mujeres en sus niveles de victimización
por el crimen.
Estos resultados, sin embargo, se tienen que comprobar formalmente
mediante una prueba de significancia, que veremos más adelante.
Apoyo a la democracia
El apoyo a la democracia, variable “ING4”, medida en una escala del 1
al 7, donde 1 significa “muy en desacuerdo” y 7 significa “muy de
acuerdo”, se tiene que recodificar. De acuerdo al reporte “Se consideran
las respuestas en la porción de la escala que indica estar de acuerdo,
esto es los valores de 5 a 7, para indicar el porcentaje que apoya a la
democracia” (p. 11). Se usa el comando mean para reportar
el promedio regional de apoyo a la democracia. Se especifica
na.rm=T para que el comando no tome en cuenta los valores
perdidos en el cálculo.
library(car)
lapop18$ing4r <- car::recode(lapop18$ing4, "1:4=0; 5:7=100")
mean(lapop18$ing4r, na.rm=T)
## [1] 57.67924
Se observa que en general, el 57.7% de entrevistados apoyo a la
democracia en el conjunto de países evaluados en 2018.
Factores asociados al apoyo a la democracia
El gráfico 1.5 muestra cómo varía el apoyo a la democracia por grupos
sociodemográficos. En particular, se presenta los resultados para la
variable lugar de residencia que distingue el ámbito urbano y rural, y
para la variable género, que distingue hombre y mujeres.
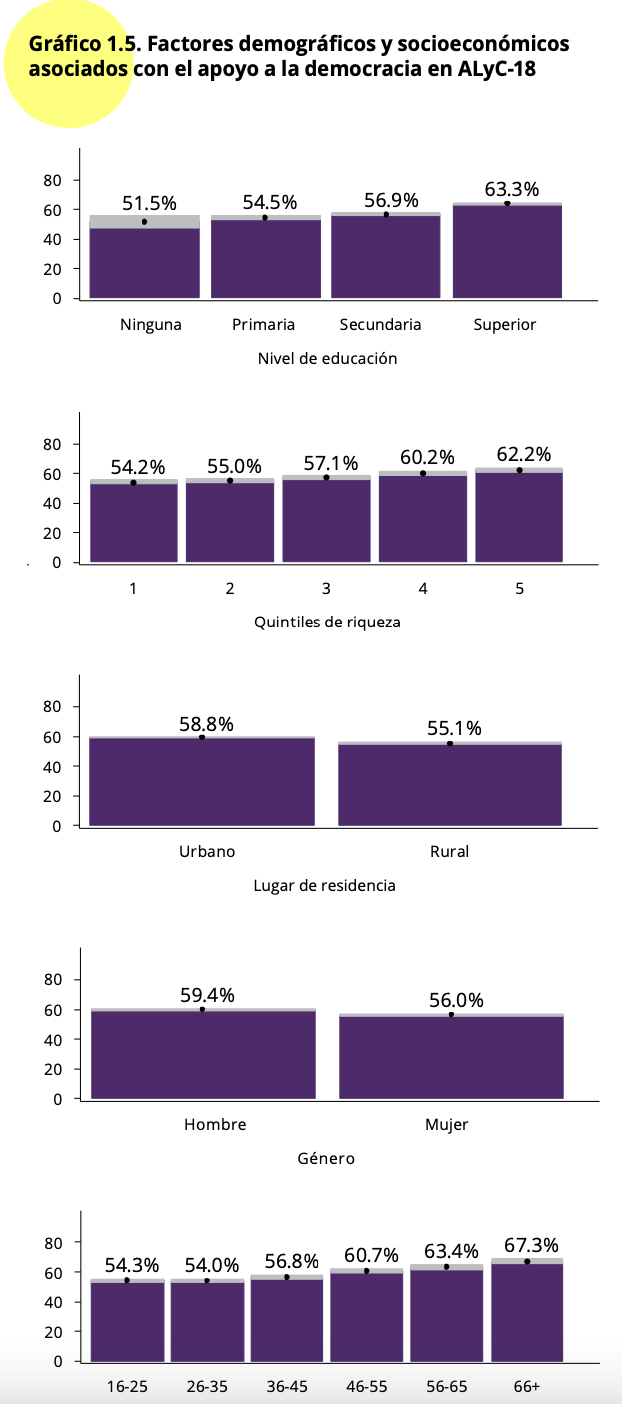
Como vimos en la sección sobre intervalos de confianza, se puede
calcular el porcentaje de apoyo por cada grupo. En primer lugar, vamos a
crear nuevas variables de factor para lugar de residencia y género, que
son importadas como variables numéricas. Estas nuevas variables luego se
etiquetan.
lapop18$genero <- as.factor(lapop18$q1)
levels(lapop18$genero) <- c("Hombre", "Mujer")
lapop18$ambito <- as.factor(lapop18$ur)
levels(lapop18$ambito) <- c("Urbano", "Rural")
De la misma manera que en el documento sobre intervalos de confianza,
usamos el comando tapply para calcular el apoyo a la
democracia promedio por grupos de género y de ámbito.
tapply(lapop18$ing4r, lapop18$genero, mean, na.rm=T) #Para género
## Hombre Mujer
## 59.42899 55.90933
tapply(lapop18$ing4r, lapop18$ambito, mean, na.rm=T) #Para urbano-rural
## Urbano Rural
## 58.71664 55.07453
Se puede reproducir los gráficos de barras que comparan el promedio
de apoyo a la democracia entre grupos de género y ámbito. Primero, para
género, se tiene que crear una tabla con los datos de la media y los
límites de los intervalos de confianza para cada grupo. Esto lo haremos
con el comando group.CI que es parte de la librería
Rmisc. Estos datos los guardamos en un objeto de tipo tabla
de R llamado “apxgen”.
Esta tabla guarda los resultados de la media de apoyo a la democracia
para cada grupo (columna “ing4r.mean”) y los límites superior e inferior
de los intervalos de confianza (columnas “ing4r.lower” y “ing4r.upper”).
También guarda la columna “genero” con los nombres de los grupos.
Se reproduce el gráfico 1.5 usando el comando ggplot de
la misma manera que en la sección anterior.
library(Rmisc)
apxgen <- group.CI(ing4r~genero, lapop18)
library(ggplot2)
graf1.5 <- ggplot(apxgen, aes(x=genero, y=ing4r.mean))+
geom_bar(width=0.5, fill="darkcyan", colour="black", stat="identity")+
geom_errorbar(aes(ymin=ing4r.lower, ymax=ing4r.upper), width=0.2)+
geom_text(aes(label=paste(round(ing4r.mean, 1), "%")), vjust=-1.5, size=4)+
xlab("Género") + ylab("Apoyo a la democracia (%)")+
ylim(0, 70)
graf1.5
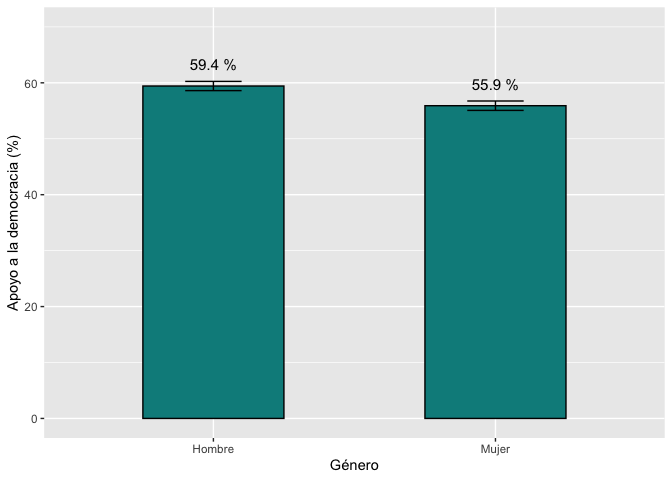
Se puede general un gráfico similar que presente el porcentaje de
apoyo a la democracia y los intervalos de confianza por grupos urbano y
rural.
apxamb <- group.CI(ing4r~ambito, lapop18)
library(ggplot2)
graf1.5_2 <- ggplot(apxamb, aes(x=ambito, y=ing4r.mean))+
geom_bar(width=0.5, fill="darkcyan", colour="black", stat="identity")+
geom_errorbar(aes(ymin=ing4r.lower, ymax=ing4r.upper), width=0.2)+
geom_text(aes(label=paste(round(ing4r.mean, 1), "%")), vjust=-1.5, size=4)+
xlab("Lugar de residencia") + ylab("Apoyo a la democracia (%)")+
ylim(0, 70)
graf1.5_2
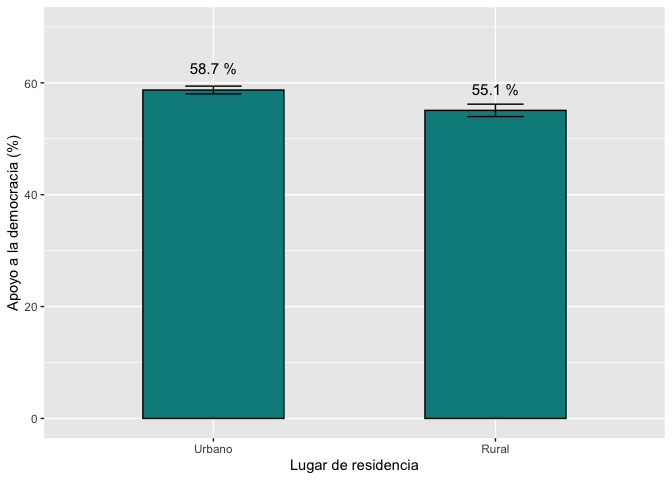
LAPOP Lab generalmente presenta en sus gráficos los intervalos de
confianza de cada grupo. Estas barras grises en el reporte sirven como
una forma de comparación rápida. Si las barras se traslapan, eso
significaría que no habrían diferencias estadísticamente significativas
entre los grupos. Por el contrario, si las barras grises no se
traslapan, se podría decir que la diferencia entre los grupos es
significativa al 95% de confianza. Sin embargo, para comprobar estas
observaciones se tiene que calcular una prueba estadística. Cuando la
comparación es entre las medias de dos grupos, la prueba estadística
apropiada es la prueba t de diferencias de medias. En esta sección
estamos asumiendo que podemos tratar a las variables “jc15a” o “ing4r”
como variables numéricas, de las que se puede calcular la media y la
desviación estándar, aunque estas variables en estricto son de tipo
cualitativa nominal.
Prueba t
La prueba t de Student pone a prueba las siguientes hipótesis:
\[
H_0: µ_1 = µ_2
\]
\[
H_a: µ_1 ≠ µ_2
\]
El estadístico de la prueba t se calcula con un error estándar que
depende de si las varianzas parecen diferentes o de si las varianzas
parecen iguales. Para determinar esta condición, lo primero es calcular
una prueba de igualdad de varianzas entre los grupos, llamada prueba de
Levene.
\[
H_0: var_1 = var_2
\]
\[
H_a: var_1 ≠ var_2
\]
Resumen
En esta sección hemos descrito y graficado, como apoyo a la
democracia, por grupos de otra variable. Partiendo de la comparación de
intervalos de confianza, formalizamos esta comparación con una prueba
estadística, como la prueba t, para concluir si las diferencias entre
grupos son estadísticamente significativas.
Cálculos incluyendo el efecto de diseño
Para victimización por crimen
Para calcular la diferencia de medias incluyendo el factor de
expansión se puede usar la librería survey. Este comando
requiere una adecuación de la base de datos, de la misma manera que se
hizo en este módulo.
lapop21 = subset(lapop21, !is.na(weight1500))
sapply(lapop21, haven::zap_labels)
Una vez adecuada la base de datos, se tiene que definir el diseño
muestral con el comando svydesign y guardar este diseño en
un objeto, aquí llamado “diseno21”.
library(survey)
diseno21 = svydesign(ids = ~upm, strata = ~strata, weights = ~weight1500, nest=TRUE, data=lapop21)
En primer lugar, se puede calcular la tabla de la media de
victimización por crimen para cada valor de la variable género
incluyendo el factor de expansión. De la misma manera que se vio en la
sección sobre intervalos
de confianza, se usa el comando svyby.
crxgen.w <- svyby(~crimen, ~genero, diseno21, svymean, na.rm=T, vartype = "ci")
crxgen.w
Se debe notar que estos resultados son iguales a los presentados en
el gráfico 3.12. Con esta tabla se puede proceder a replicar el gráfico
de barras del panel izquierdo de ese gráfico, de la misma manera que se
realizó arriba en esta sección.
Para el cálculo de la prueba t de diferencia de medias, el paquete
survey cuenta con un comando nativo que permite hacer este
calculo svyttest. Sin embargo, en este caso no se cuenta
con un comando para evaluar la igualdad de varianzas, como el
LeveneTest. El comando svyttest es una
derivación de un comando más general para modelos lineales
generalizados, que asumen igualdad de varianzas. Si se quisiera
comprobar este supuesto, se puede hacer de manera manual, tal como se
indica en este link.
Aquí se va a proceder asumiendo el supuesto. Se observa que el comando
regresa resultados muy parecidos al comando sin el efecto de diseño y
para todo efecto se llegan a las mismas conclusiones. El p-value es
menor a 0.05, por lo que se puede rechazar la H0 de igualdad de medias y
afirmar que existe una diferencia en el apoyo a la democracia entre
hombres y mujeres en la población, tomando en cuenta el efecto de
diseño.
svyttest(crimen~genero, diseno21)
##
## Design-based t-test
##
## data: crimen ~ genero
## t = 4.3654, df = 30282, p-value = 1.273e-05
## alternative hypothesis: true difference in mean is not equal to 0
## 95 percent confidence interval:
## 1.370025 3.602805
## sample estimates:
## difference in mean
## 2.486415
Como el p-value es menor a 0.05, se concluye que existen diferencias
entre hombre y mujeres en sus niveles de victimización por el crimen en
toda la región.
Para apoyo a la democracia
De la misma manera que en el ejemplo anterior, en primer lugar se
define el efecto de diseño y se guarda en un objeto “diseno18”.
library(survey)
diseno18<-svydesign(ids = ~upm, strata = ~estratopri, weights = ~weight1500, nest=TRUE, data=lapop18)
Luego, se usa el comando svyby para calcular la media de
apoyo a la democracia por grupos de género.
apxgen.w <- svyby(~ing4r, ~genero, diseno18, svymean, na.rm=T, vartype = "ci")
apxgen.w
Con esta tabla se puede proceder a crear el gráfico de barras, de la
misma manera que se realizó arriba en esta sección.
Igual que en el ejemplo anterior, se procede a usar el comando nativo
svyttest para evaluar la diferencia de medias de apoyo a la
democracia entre hombres y mujeres.
svyttest(ing4r~genero, diseno18)
##
## Design-based t-test
##
## data: ing4r ~ genero
## t = -5.8332, df = 1329, p-value = 6.822e-09
## alternative hypothesis: true difference in mean is not equal to 0
## 95 percent confidence interval:
## -4.672004 -2.320395
## sample estimates:
## difference in mean
## -3.496199
Como el p-value es menor a 0.05, se concluye que sí existen
diferencias entre hombre y mujeres en el apoyo a la democracia en toda
la región.
LS0tCnRpdGxlOiAiQ29tcGFyYWNpw7NuIGRlIDIgbWVkaWFzIGNvbiBlbCBCYXLDs21ldHJvIGRlIGxhcyBBbcOpcmljYXMiCm91dHB1dDoKICBodG1sX2RvY3VtZW50OgogICAgdG9jOiB0cnVlCiAgICB0b2NfZmxvYXQ6IHRydWUKICAgIGNvbGxhcHNlZDogZmFsc2UKICAgIG51bWJlcl9zZWN0aW9uczogZmFsc2UKICAgIHRvY19kZXB0aDogMQogICAgY29kZV9kb3dubG9hZDogdHJ1ZQogICAgdGhlbWU6IGZsYXRseQogICAgZGZfcHJpbnQ6IHBhZ2VkCiAgICBzZWxmX2NvbnRhaW5lZDogbm8KICAgIGtlZXBfbWQ6IHllcwplZGl0b3Jfb3B0aW9uczogCiAgbWFya2Rvd246IAogICAgd3JhcDogc2VudGVuY2UKLS0tCgpgYGB7ciBzZXR1cCwgaW5jbHVkZT1GQUxTRX0Ka25pdHI6Om9wdHNfY2h1bmskc2V0KG1lc3NhZ2U9RkFMU0Usd2FybmluZz1GQUxTRSwgY2FjaGU9VFJVRSkKYGBgCgpgYGB7Y3NzIGNvbG9yLCBlY2hvPUZBTFNFfQouY29sdW1ucyB7ZGlzcGxheTogZmxleDt9CmgxIHtjb2xvcjogIzMzNjZDQzt9CmBgYAoKIyBJbnRyb2R1Y2Npw7NuCgpFbiBlc3RlIGRvY3VtZW50byB2ZXJlbW9zIGNvbW8gY29tcGFyYXIgZG9zIG1lZGlhcyB5IHNhYmVyIHNpIGxhcyBkaWZlcmVuY2lhcyBzZSBwdWVkZW4gaW5mZXJpciBhIGxhIHBvYmxhY2nDs24sIG1lZGlhbnRlIGxhIHBydWViYSB0IGRlIGNvbXBhcmFjacOzbiBkZSBtZWRpYXMuClBhcmEgZXNvLCB2YW1vcyBhIHNlZ3VpciB1c2FuZG8gbG9zIMO6bHRpbW9zIHJlcG9ydGVzICJFbCBwdWxzbyBkZSBsYSBkZW1vY3JhY2lhIiwgZGVsIDIwMjEsIGRpc3BvbmlibGUgW2FxdcOtXShodHRwczovL3d3dy52YW5kZXJiaWx0LmVkdS9sYXBvcC9hYjIwMjEvMjAyMV9MQVBPUF9BbWVyaWNhc0Jhcm9tZXRlcl9QdWxzZV9vZl9EZW1vY3JhY3kucGRmKSwgeSBkZWwgMjAxOC8xOSwgZGlzcG9uaWJsZSBbYXF1w61dKGh0dHBzOi8vd3d3LnZhbmRlcmJpbHQuZWR1L2xhcG9wL2FiMjAxOC8yMDE4LTE5X0FtZXJpY2FzQmFyb21ldGVyX1JlZ2lvbmFsX1JlcG9ydF9TcGFuaXNoX1dfMDMuMjcuMjAucGRmKSwgZG9uZGUgc2UgcHJlc2VudGFuIGxvcyBwcmluY2lwYWxlcyBoYWxsYXpnb3MgZGVsIEJhcsOzbWV0cm8gZGUgbGFzIEFtw6lyaWNhcy4KCkVuIGVsIHJlcG9ydGUgMjAyMSBzZSBwcmVzZW50YW4gbG9zIHJlc3VsdGFkb3Mgc29icmUgbGEgdmljdGltaXphY2nDs24gcG9yIGVsIGNyaW1lbiBwb3IgZ3J1cG9zIGRlIGfDqW5lcm8sIGVkYWQsIGVkdWNhY2nDs24geSByaXF1ZXphICh2ZXIgR3LDoWZpY28gMy4xMikuCkVuIGVsIGluZm9ybWUgZGUgbGEgcm9uZGEgMjAxOC8xOSBzZSByZXBvcnRhbiBsb3MgcmVzdWx0YWRvcyBzb2JyZSBhcG95byBhIGxhIGRlbW9jcmFjaWEgZWxlY3RvcmFsLCB2YXJpYWJsZSBxdWUgc2UgY3J1emEgY29uIGFsZ3VuYXMgb3RyYXMgdmFyaWFibGVzIHNvY2lvZGVtb2dyw6FmaWNhcyBjb21vIHNleG8gbyBsdWdhciBkZSByZXNpZGVuY2lhICh2ZXIgR3LDoWZpY28gMS41KS4KCkVuIGVzdGEgc2VjY2nDs24gYW5hbGl6YXJlbW9zIGxvcyBjYXNvcyBjdWFuZG8gbGEgdmljdGltaXphY2nDs24gcG9yIGVsIGNyaW1lbiBzZSBjb21wYXJhIGVudHJlIGhvbWJyZXMgeSBtdWplcmVzIHkgY3VhbmRvIGVsIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSBzZSBjb21wYXJhIGVudHJlIGdydXBvcyBkZSBnw6luZXJvIHkgZGUgcmVzaWRlbmNpYSB1cmJhbmEgbyBydXJhbC4KCiMgU29icmUgbGEgYmFzZSBkZSBkYXRvcwoKTG9zIGRhdG9zIHF1ZSB2YW1vcyBhIHVzYXIgZGViZW4gY2l0YXJzZSBkZSBsYSBzaWd1aWVudGUgbWFuZXJhOiBGdWVudGU6IEJhcsOzbWV0cm8gZGUgbGFzIEFtw6lyaWNhcyBwb3IgZWwgUHJveWVjdG8gZGUgT3BpbmnDs24gUMO6YmxpY2EgZGUgQW3DqXJpY2EgTGF0aW5hIChMQVBPUCksIHd3d3cuTGFwb3BTdXJ2ZXlzLm9yZy4KRW4gZXN0ZSBkb2N1bWVudG8gc2UgY2FyZ2EgdW5hIGJhc2UgZGUgZGF0b3MgcmVjb3J0YWRhLgpFc3RhIGJhc2UgZGUgZGF0b3Mgc2UgZW5jdWVudHJhIGFsb2phZGEgZW4gZWwgcmVwb3NpdG9yaW8gIm1hdGVyaWFsc19lZHUiIGRlIGxhIGN1ZW50YSBkZSBMQVBPUCBlbiBHaXRIdWIuClNlIHJlY29taWVuZG8gbGltcGlhciBlbCBFbnZpcm9ubWVudCBhbnRlcyBkZSBwcm9jZWRlciBjb24gZXN0YSBzZWNjacOzbi4KCk1lZGlhbnRlIGxhIGxpYnJlcsOtYSBgcmlvYCB5IGVsIGNvbWFuZG8gYGltcG9ydGAgc2UgcHVlZGUgaW1wb3J0YXIgZXN0YSBiYXNlIGRlIGRhdG9zIGRlc2RlIGVzdGUgcmVwb3NpdG9yaW8uCkFkZW3DoXMsIHNlIHNlbGVjY2lvbmFuIGxvcyBkYXRvcyBkZSBwYcOtc2VzIGNvbiBjw7NkaWdvcyBtZW5vcmVzIG8gaWd1YWxlcyBhIDM1LCBlcyBkZWNpciwgc2UgZWxpbWluYSBsYXMgb2JzZXJ2YWNpb25lcyBkZSBFc3RhZG9zIFVuaWRvcyB5IENhbmFkw6EuCgpgYGB7ciBiYXNlMTh9CmxpYnJhcnkocmlvKSAKbGFwb3AxOCA8LSBpbXBvcnQoImh0dHBzOi8vcmF3LmdpdGh1Yi5jb20vbGFwb3AtY2VudHJhbC9tYXRlcmlhbHNfZWR1L21haW4vTEFQT1BfQUJfTWVyZ2VfMjAxOF92MS4wLnNhdiIpIApsYXBvcDE4IDwtIHN1YnNldChsYXBvcDE4LCBwYWlzPD0zNSkKYGBgCgpUYW1iacOpbiBjYXJnYW1vcyBsYSBiYXNlIGRlIGRhdG9zIGRlIGxhIHJvbmRhIDIwMjEuCgpgYGB7ciBiYXNlMjF9CmxhcG9wMjEgPSBpbXBvcnQoImxhcG9wMjEuUkRhdGEiKSAKbGFwb3AyMSA8LSBzdWJzZXQobGFwb3AyMSwgcGFpczw9MzUpCmBgYAoKIyBWaWN0aW1pemFjacOzbiBwb3IgZWwgY3JpbWVuCgpMYSB2aWN0aW1pemFjacOzbiBwb3IgZWwgY3JpbWVuIGVzdMOhIG1lZGlkYSBjb24gbGEgdmFyaWFibGUgInZpYzFleHQiLgpMYSBwcmVndW50YSBlc3TDoSBmcmFzZWFkYTogIkFob3JhLCBjYW1iaWFuZG8gZGUgdGVtYSwgwr9oYSBzaWRvIHVzdGVkIHbDrWN0aW1hIGRlIGFsZ8O6biBhY3RvIGRlIGRlbGluY3VlbmNpYSBlbiBsb3Mgw7psdGltb3MgMTIgbWVzZXM/IEVzIGRlY2lyLCDCv2hhIHNpZG8gdsOtY3RpbWEgZGUgdW4gcm9ibywgaHVydG8sIGFncmVzacOzbiwgZnJhdWRlLCBjaGFudGFqZSwgZXh0b3JzacOzbiwgYW1lbmF6YXMgbyBhbGfDum4gb3RybyB0aXBvIGRlIGFjdG8gZGVsaW5jdWVuY2lhbCBlbiBsb3Mgw7psdGltb3MgMTIgbWVzZXM/Ii4KCkVzdGEgdmFyaWFibGUgZXN0w6EgY29kaWZpY2FkYSBjb21vIDEgIlPDrSIgeSAyICJOby4gUGFyYSBwb2RlciByZXBsaWNhciBsb3MgcmVzdWx0YWRvcyBkZWwgZ3LDoWZpY28gMy4xMiB0ZW5lbW9zIHF1ZSByZWNvZGlmaWNhciBlc3RhIHZhcmlhYmxlLiBDb21vIGluZGljYW1vcyBlbiBlbCBtw7NkdWxvIGFudGVyaW9yLCBlc3RhIGNvZGlmaWNhY2nDs24gbm9zIHBlcm1pdGUgY2FsY3VsYXIgZWwgcG9yY2VudGFqZSBkZSB2w61jdGltYXMgZGVsIGNyaW1lbiBtZWRpYW50ZSBlbCBjb21hbmRvIGBtZWFuYC4gRWwgcmVzdWx0YWRvIG5vcyBpbmRpY2EgcXVlIGVsIDIyJSBkZSBjaXVkYWRhbm9zIGVuIGxhIHJlZ2nDs24gcmVwb3J0YSBoYWJlciBzaWRvIHbDrWN0aW1hIGRlbCBjcmltZW4uCgpgYGB7ciByZWNvZGlmaWNhY2lvbiBjcmltZW59CmxpYnJhcnkoY2FyKQpsYXBvcDIxJGNyaW1lbiA8LSBjYXI6OnJlY29kZShsYXBvcDIxJHZpYzFleHQsICIxPTEwMDsgMj0wIikKbWVhbihsYXBvcDIxJGNyaW1lbiwgbmEucm09VCkKYGBgCgpFbCBncsOhZmljbyAzLjEyIG11ZXN0cmEgbGEgY29tcGFyYWNpw7NuIGRlIGxhIHZpY3RpbWl6YWNpw7NuIHBvciBlbCBjcmltZW4gY3J1emFkYSBwb3IgY3VhdHJvIHZhcmlhYmxlcyBzb2Npb2RlbW9ncsOhZmljYXM6IGfDqW5lcm8sIGVkYWQsIGVkdWNhY2nDs24geSBxdWludGlsZXMgZGUgcmlxdWV6YS4KCiFbXShGaWd1cmUzLjEyLnBuZyl7d2lkdGg9IjUzNCJ9CgpQYXJhIHJlcGxpY2FyIGxhcyBkaWZlcmVuY2lhcyBlbnRyZSBnw6luZXJvcywgc2UgdGllbmUgcXVlIHJlY29kaWZpY2FyIGxhIHZhcmlhYmxlICJxMXRiIiB5IGx1ZWdvIGRlY2xhcmFybGEgY29tbyBmYWN0b3IuCgpgYGB7ciBmYWN0b3IgY3JpbWVufQpsYXBvcDIxJGdlbmVybyA9IGNhcjo6cmVjb2RlKGxhcG9wMjEkcTF0YiwgIjE9MjsgMj0xOyAzPTEiKQpsYXBvcDIxJGdlbmVybyA9IGFzLmZhY3RvcihsYXBvcDIxJGdlbmVybykKbGV2ZWxzKGxhcG9wMjEkZ2VuZXJvKSA9IGMoIk11amVyIiwgIkhvbWJyZSIpCnRhYmxlKGxhcG9wMjEkZ2VuZXJvKQpgYGAKCkRlIGxhIG1pc21hIG1hbmVyYSBxdWUgZW4gZWwgZG9jdW1lbnRvIHNvYnJlIGludGVydmFsb3MgZGUgY29uZmlhbnphLCB1c2Ftb3MgZWwgY29tYW5kbyBgdGFwcGx5YCBwYXJhIGNhbGN1bGFyIGVsIHBvcmNlbnRhamUgZGUgdmljdGltaXphY2nDs24gcG9yIGNyaW1lbiBwb3IgZ3J1cG9zIGRlIGfDqW5lcm8uCgpgYGB7ciBjcmltZW4gcG9yIGdlbmVyb30KIHRhcHBseShsYXBvcDIxJGNyaW1lbiwgbGFwb3AyMSRnZW5lcm8sIG1lYW4sIG5hLnJtPVQpICNQYXJhIGfDqW5lcm8KYGBgCgpQYXJhIHJlcHJvZHVjaXIgZWwgZ3LDoWZpY28gZGUgYmFycmFzLCBpbmNsdXllbmRvIGxvcyBpbnRlcnZhbG9zIGRlIGNvbmZpYW56YSwgcHJpbWVybyBzZSBwdWVkZSBwcm9kdWNpciB1bmEgdGFibGEgcXVlIGd1YXJkZSBlbCB2YWxvciBkZWwgcG9yY2VudGFqZSBkZSBjYWRhIGdydXBvLCBhc8OtIGNvbW8gZWwgdmFsb3IgaW5mZXJpb3IgeSBzdXBlcmlvciBkZWwgaW50ZXJ2YWxvIGRlIGNvbmZpYW56YS4KRXN0byBzZSBwdWVkZSBoYWNlciBjb24gZWwgY29tYW5kbyBgZ3JvdXAuQ0lgIGRlbCBwYXF1ZXRlIGBSbWlzY2AuCgpDb24gZXN0YSB0YWJsZSwgc2UgcHVlZGUgdXNhciBsYSBsaWJyZXLDrWEgYGdncGxvdGAgcGFyYSByZXByb2R1Y2lyIGVsIHByaW1lciBwYW5lbCBkZWwgZ3LDoWZpY28gMy4xMi4KTG9zIHJlc3VsdGFkb3Mgbm8gc29uIGlkw6ludGljb3MgZGFkbyBxdWUgbm8gc2UgaGEgdXNhZG8gZWwgZWZlY3RvIGRlIGRpc2XDsW8uCgpgYGB7ciBncmFmaWNvIGNyaW1lbiBwb3IgZ2VuZXJvfQpsaWJyYXJ5KFJtaXNjKQpjcnhnZW4gPC0gZ3JvdXAuQ0koY3JpbWVufmdlbmVybywgbGFwb3AyMSkKbGlicmFyeShnZ3Bsb3QyKQpncmFmMy4xMmEgPC0gZ2dwbG90KGNyeGdlbiwgYWVzKHg9Z2VuZXJvLCB5PWNyaW1lbi5tZWFuKSkrCiAgZ2VvbV9iYXIod2lkdGg9MC41LCBmaWxsPSJkYXJrY3lhbiIsIGNvbG91cj0iYmxhY2siLCBzdGF0PSJpZGVudGl0eSIpKwogIGdlb21fZXJyb3JiYXIoYWVzKHltaW49Y3JpbWVuLmxvd2VyLCB5bWF4PWNyaW1lbi51cHBlciksIHdpZHRoPTAuMikrCiAgZ2VvbV90ZXh0KGFlcyhsYWJlbD1wYXN0ZShyb3VuZChjcmltZW4ubWVhbiwgMSksICIlIikpLCB2anVzdD0tMS41LCBzaXplPTQpKwogIHhsYWIoIkfDqW5lcm8iKSArIHlsYWIoIlZpY3RpbWl6YWNpw7NuIHBvciBjcmltZW4gKCUpIikrCiAgeWxpbSgwLCA0MCkKZ3JhZjMuMTJhCmBgYAoKRW4gZXN0ZSBncsOhZmljbyBzZSBwdWVkZSBjb21wYXJhciB2aXN1YWxtZW50ZSBsb3MgaW50ZXJ2YWxvcyBkZSBjb25maWFuemEgZGUgY2FkYSBncnVwby4KQ29tbyBlc3RvcyBubyBzZSB0cmFzbGFwYW4sIHNlIHB1ZWRlIGNvbmNsdWlyIGRlIG1hbmVyYSBpbmljaWFsIHF1ZSBleGlzdGVuIGRpZmVyZW5jaWFzIGVzdGFkw61zdGljYW1lbnRlIHNpZ25pZmljYXRpdmFzIGVudHJlIGhvbWJyZXMgeSBtdWplcmVzIGVuIHN1cyBuaXZlbGVzIGRlIHZpY3RpbWl6YWNpw7NuIHBvciBlbCBjcmltZW4uCgpFc3RvcyByZXN1bHRhZG9zLCBzaW4gZW1iYXJnbywgc2UgdGllbmVuIHF1ZSBjb21wcm9iYXIgZm9ybWFsbWVudGUgbWVkaWFudGUgdW5hIHBydWViYSBkZSBzaWduaWZpY2FuY2lhLCBxdWUgdmVyZW1vcyBtw6FzIGFkZWxhbnRlLgoKIyBBcG95byBhIGxhIGRlbW9jcmFjaWEKCkVsIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSwgdmFyaWFibGUgIklORzQiLCBtZWRpZGEgZW4gdW5hIGVzY2FsYSBkZWwgMSBhbCA3LCBkb25kZSAxIHNpZ25pZmljYSAibXV5IGVuIGRlc2FjdWVyZG8iIHkgNyBzaWduaWZpY2EgIm11eSBkZSBhY3VlcmRvIiwgc2UgdGllbmUgcXVlIHJlY29kaWZpY2FyLgpEZSBhY3VlcmRvIGFsIHJlcG9ydGUgIlNlIGNvbnNpZGVyYW4gbGFzIHJlc3B1ZXN0YXMgZW4gbGEgcG9yY2nDs24gZGUgbGEgZXNjYWxhIHF1ZSBpbmRpY2EgZXN0YXIgZGUgYWN1ZXJkbywgZXN0byBlcyBsb3MgdmFsb3JlcyBkZSA1IGEgNywgcGFyYSBpbmRpY2FyIGVsIHBvcmNlbnRhamUgcXVlIGFwb3lhIGEgbGEgZGVtb2NyYWNpYSIgKHAuIDExKS4KU2UgdXNhIGVsIGNvbWFuZG8gYG1lYW5gIHBhcmEgcmVwb3J0YXIgZWwgcHJvbWVkaW8gcmVnaW9uYWwgZGUgYXBveW8gYSBsYSBkZW1vY3JhY2lhLgpTZSBlc3BlY2lmaWNhIGBuYS5ybT1UYCBwYXJhIHF1ZSBlbCBjb21hbmRvIG5vIHRvbWUgZW4gY3VlbnRhIGxvcyB2YWxvcmVzIHBlcmRpZG9zIGVuIGVsIGPDoWxjdWxvLgoKYGBge3IgcmVjb2RpZmljYXJ9CmxpYnJhcnkoY2FyKQpsYXBvcDE4JGluZzRyIDwtIGNhcjo6cmVjb2RlKGxhcG9wMTgkaW5nNCwgIjE6ND0wOyA1Ojc9MTAwIikKbWVhbihsYXBvcDE4JGluZzRyLCBuYS5ybT1UKQpgYGAKClNlIG9ic2VydmEgcXVlIGVuIGdlbmVyYWwsIGVsIDU3LjclIGRlIGVudHJldmlzdGFkb3MgYXBveW8gYSBsYSBkZW1vY3JhY2lhIGVuIGVsIGNvbmp1bnRvIGRlIHBhw61zZXMgZXZhbHVhZG9zIGVuIDIwMTguCgojIyBGYWN0b3JlcyBhc29jaWFkb3MgYWwgYXBveW8gYSBsYSBkZW1vY3JhY2lhCgpFbCBncsOhZmljbyAxLjUgbXVlc3RyYSBjw7NtbyB2YXLDrWEgZWwgYXBveW8gYSBsYSBkZW1vY3JhY2lhIHBvciBncnVwb3Mgc29jaW9kZW1vZ3LDoWZpY29zLgpFbiBwYXJ0aWN1bGFyLCBzZSBwcmVzZW50YSBsb3MgcmVzdWx0YWRvcyBwYXJhIGxhIHZhcmlhYmxlIGx1Z2FyIGRlIHJlc2lkZW5jaWEgcXVlIGRpc3Rpbmd1ZSBlbCDDoW1iaXRvIHVyYmFubyB5IHJ1cmFsLCB5IHBhcmEgbGEgdmFyaWFibGUgZ8OpbmVybywgcXVlIGRpc3Rpbmd1ZSBob21icmUgeSBtdWplcmVzLgoKIVtdKEdyYWYxLjUucG5nKXt3aWR0aD0iMzMzIn0KCkNvbW8gdmltb3MgZW4gbGEgc2VjY2nDs24gc29icmUgaW50ZXJ2YWxvcyBkZSBjb25maWFuemEsIHNlIHB1ZWRlIGNhbGN1bGFyIGVsIHBvcmNlbnRhamUgZGUgYXBveW8gcG9yIGNhZGEgZ3J1cG8uCkVuIHByaW1lciBsdWdhciwgdmFtb3MgYSBjcmVhciBudWV2YXMgdmFyaWFibGVzIGRlIGZhY3RvciBwYXJhIGx1Z2FyIGRlIHJlc2lkZW5jaWEgeSBnw6luZXJvLCBxdWUgc29uIGltcG9ydGFkYXMgY29tbyB2YXJpYWJsZXMgbnVtw6lyaWNhcy4KRXN0YXMgbnVldmFzIHZhcmlhYmxlcyBsdWVnbyBzZSBldGlxdWV0YW4uCgpgYGB7ciBmYWN0b3Jlc30KbGFwb3AxOCRnZW5lcm8gPC0gYXMuZmFjdG9yKGxhcG9wMTgkcTEpCmxldmVscyhsYXBvcDE4JGdlbmVybykgPC0gYygiSG9tYnJlIiwgIk11amVyIikKbGFwb3AxOCRhbWJpdG8gPC0gYXMuZmFjdG9yKGxhcG9wMTgkdXIpCmxldmVscyhsYXBvcDE4JGFtYml0bykgPC0gYygiVXJiYW5vIiwgIlJ1cmFsIikKYGBgCgpEZSBsYSBtaXNtYSBtYW5lcmEgcXVlIGVuIGVsIGRvY3VtZW50byBzb2JyZSBpbnRlcnZhbG9zIGRlIGNvbmZpYW56YSwgdXNhbW9zIGVsIGNvbWFuZG8gYHRhcHBseWAgcGFyYSBjYWxjdWxhciBlbCBhcG95byBhIGxhIGRlbW9jcmFjaWEgcHJvbWVkaW8gcG9yIGdydXBvcyBkZSBnw6luZXJvIHkgZGUgw6FtYml0by4KCmBgYHtyIGFwb3lvIHBvciBncnVwb3N9CnRhcHBseShsYXBvcDE4JGluZzRyLCBsYXBvcDE4JGdlbmVybywgbWVhbiwgbmEucm09VCkgI1BhcmEgZ8OpbmVybwp0YXBwbHkobGFwb3AxOCRpbmc0ciwgbGFwb3AxOCRhbWJpdG8sIG1lYW4sIG5hLnJtPVQpICNQYXJhIHVyYmFuby1ydXJhbApgYGAKClNlIHB1ZWRlIHJlcHJvZHVjaXIgbG9zIGdyw6FmaWNvcyBkZSBiYXJyYXMgcXVlIGNvbXBhcmFuIGVsIHByb21lZGlvIGRlIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSBlbnRyZSBncnVwb3MgZGUgZ8OpbmVybyB5IMOhbWJpdG8uClByaW1lcm8sIHBhcmEgZ8OpbmVybywgc2UgdGllbmUgcXVlIGNyZWFyIHVuYSB0YWJsYSBjb24gbG9zIGRhdG9zIGRlIGxhIG1lZGlhIHkgbG9zIGzDrW1pdGVzIGRlIGxvcyBpbnRlcnZhbG9zIGRlIGNvbmZpYW56YSBwYXJhIGNhZGEgZ3J1cG8uCkVzdG8gbG8gaGFyZW1vcyBjb24gZWwgY29tYW5kbyBgZ3JvdXAuQ0lgIHF1ZSBlcyBwYXJ0ZSBkZSBsYSBsaWJyZXLDrWEgYFJtaXNjYC4KRXN0b3MgZGF0b3MgbG9zIGd1YXJkYW1vcyBlbiB1biBvYmpldG8gZGUgdGlwbyB0YWJsYSBkZSBSIGxsYW1hZG8gImFweGdlbiIuCgpFc3RhIHRhYmxhIGd1YXJkYSBsb3MgcmVzdWx0YWRvcyBkZSBsYSBtZWRpYSBkZSBhcG95byBhIGxhIGRlbW9jcmFjaWEgcGFyYSBjYWRhIGdydXBvIChjb2x1bW5hICJpbmc0ci5tZWFuIikgeSBsb3MgbMOtbWl0ZXMgc3VwZXJpb3IgZSBpbmZlcmlvciBkZSBsb3MgaW50ZXJ2YWxvcyBkZSBjb25maWFuemEgKGNvbHVtbmFzICJpbmc0ci5sb3dlciIgeSAiaW5nNHIudXBwZXIiKS4KVGFtYmnDqW4gZ3VhcmRhIGxhIGNvbHVtbmEgImdlbmVybyIgY29uIGxvcyBub21icmVzIGRlIGxvcyBncnVwb3MuCgpTZSByZXByb2R1Y2UgZWwgZ3LDoWZpY28gMS41IHVzYW5kbyBlbCBjb21hbmRvIGBnZ3Bsb3RgIGRlIGxhIG1pc21hIG1hbmVyYSBxdWUgZW4gbGEgc2VjY2nDs24gYW50ZXJpb3IuCgpgYGB7ciBhcG95b3hnZW59CmxpYnJhcnkoUm1pc2MpCmFweGdlbiA8LSBncm91cC5DSShpbmc0cn5nZW5lcm8sIGxhcG9wMTgpCmxpYnJhcnkoZ2dwbG90MikKZ3JhZjEuNSA8LSBnZ3Bsb3QoYXB4Z2VuLCBhZXMoeD1nZW5lcm8sIHk9aW5nNHIubWVhbikpKwogIGdlb21fYmFyKHdpZHRoPTAuNSwgZmlsbD0iZGFya2N5YW4iLCBjb2xvdXI9ImJsYWNrIiwgc3RhdD0iaWRlbnRpdHkiKSsKICBnZW9tX2Vycm9yYmFyKGFlcyh5bWluPWluZzRyLmxvd2VyLCB5bWF4PWluZzRyLnVwcGVyKSwgd2lkdGg9MC4yKSsKICBnZW9tX3RleHQoYWVzKGxhYmVsPXBhc3RlKHJvdW5kKGluZzRyLm1lYW4sIDEpLCAiJSIpKSwgdmp1c3Q9LTEuNSwgc2l6ZT00KSsKICB4bGFiKCJHw6luZXJvIikgKyB5bGFiKCJBcG95byBhIGxhIGRlbW9jcmFjaWEgKCUpIikrCiAgeWxpbSgwLCA3MCkKZ3JhZjEuNQpgYGAKClNlIHB1ZWRlIGdlbmVyYWwgdW4gZ3LDoWZpY28gc2ltaWxhciBxdWUgcHJlc2VudGUgZWwgcG9yY2VudGFqZSBkZSBhcG95byBhIGxhIGRlbW9jcmFjaWEgeSBsb3MgaW50ZXJ2YWxvcyBkZSBjb25maWFuemEgcG9yIGdydXBvcyB1cmJhbm8geSBydXJhbC4KCmBgYHtyIGFwb3lveGFtYn0KYXB4YW1iIDwtIGdyb3VwLkNJKGluZzRyfmFtYml0bywgbGFwb3AxOCkKbGlicmFyeShnZ3Bsb3QyKQpncmFmMS41XzIgPC0gZ2dwbG90KGFweGFtYiwgYWVzKHg9YW1iaXRvLCB5PWluZzRyLm1lYW4pKSsKICBnZW9tX2Jhcih3aWR0aD0wLjUsIGZpbGw9ImRhcmtjeWFuIiwgY29sb3VyPSJibGFjayIsIHN0YXQ9ImlkZW50aXR5IikrCiAgZ2VvbV9lcnJvcmJhcihhZXMoeW1pbj1pbmc0ci5sb3dlciwgeW1heD1pbmc0ci51cHBlciksIHdpZHRoPTAuMikrCiAgZ2VvbV90ZXh0KGFlcyhsYWJlbD1wYXN0ZShyb3VuZChpbmc0ci5tZWFuLCAxKSwgIiUiKSksIHZqdXN0PS0xLjUsIHNpemU9NCkrCiAgeGxhYigiTHVnYXIgZGUgcmVzaWRlbmNpYSIpICsgeWxhYigiQXBveW8gYSBsYSBkZW1vY3JhY2lhICglKSIpKwogIHlsaW0oMCwgNzApCmdyYWYxLjVfMgpgYGAKCkxBUE9QIExhYiBnZW5lcmFsbWVudGUgcHJlc2VudGEgZW4gc3VzIGdyw6FmaWNvcyBsb3MgaW50ZXJ2YWxvcyBkZSBjb25maWFuemEgZGUgY2FkYSBncnVwby4KRXN0YXMgYmFycmFzIGdyaXNlcyBlbiBlbCByZXBvcnRlIHNpcnZlbiBjb21vIHVuYSBmb3JtYSBkZSBjb21wYXJhY2nDs24gcsOhcGlkYS4KU2kgbGFzIGJhcnJhcyBzZSB0cmFzbGFwYW4sIGVzbyBzaWduaWZpY2Fyw61hIHF1ZSBubyBoYWJyw61hbiBkaWZlcmVuY2lhcyBlc3RhZMOtc3RpY2FtZW50ZSBzaWduaWZpY2F0aXZhcyBlbnRyZSBsb3MgZ3J1cG9zLgpQb3IgZWwgY29udHJhcmlvLCBzaSBsYXMgYmFycmFzIGdyaXNlcyBubyBzZSB0cmFzbGFwYW4sIHNlIHBvZHLDrWEgZGVjaXIgcXVlIGxhIGRpZmVyZW5jaWEgZW50cmUgbG9zIGdydXBvcyBlcyBzaWduaWZpY2F0aXZhIGFsIDk1JSBkZSBjb25maWFuemEuClNpbiBlbWJhcmdvLCBwYXJhIGNvbXByb2JhciBlc3RhcyBvYnNlcnZhY2lvbmVzIHNlIHRpZW5lIHF1ZSBjYWxjdWxhciB1bmEgcHJ1ZWJhIGVzdGFkw61zdGljYS4KQ3VhbmRvIGxhIGNvbXBhcmFjacOzbiBlcyBlbnRyZSBsYXMgbWVkaWFzIGRlIGRvcyBncnVwb3MsIGxhIHBydWViYSBlc3RhZMOtc3RpY2EgYXByb3BpYWRhIGVzIGxhIHBydWViYSB0IGRlIGRpZmVyZW5jaWFzIGRlIG1lZGlhcy4KRW4gZXN0YSBzZWNjacOzbiBlc3RhbW9zIGFzdW1pZW5kbyBxdWUgcG9kZW1vcyB0cmF0YXIgYSBsYXMgdmFyaWFibGVzICJqYzE1YSIgbyAiaW5nNHIiIGNvbW8gdmFyaWFibGVzIG51bcOpcmljYXMsIGRlIGxhcyBxdWUgc2UgcHVlZGUgY2FsY3VsYXIgbGEgbWVkaWEgeSBsYSBkZXN2aWFjacOzbiBlc3TDoW5kYXIsIGF1bnF1ZSBlc3RhcyB2YXJpYWJsZXMgZW4gZXN0cmljdG8gc29uIGRlIHRpcG8gY3VhbGl0YXRpdmEgbm9taW5hbC4KCiMgUHJ1ZWJhIHQKCkxhIHBydWViYSB0IGRlIFN0dWRlbnQgcG9uZSBhIHBydWViYSBsYXMgc2lndWllbnRlcyBoaXDDs3Rlc2lzOgoKJCQKSF8wOiDCtV8xID0gwrVfMgokJAoKJCQKSF9hOiDCtV8xIOKJoCDCtV8yCiQkCgpFbCBlc3RhZMOtc3RpY28gZGUgbGEgcHJ1ZWJhIHQgc2UgY2FsY3VsYSBjb24gdW4gZXJyb3IgZXN0w6FuZGFyIHF1ZSBkZXBlbmRlIGRlIHNpIGxhcyB2YXJpYW56YXMgcGFyZWNlbiBkaWZlcmVudGVzIG8gZGUgc2kgbGFzIHZhcmlhbnphcyBwYXJlY2VuIGlndWFsZXMuClBhcmEgZGV0ZXJtaW5hciBlc3RhIGNvbmRpY2nDs24sIGxvIHByaW1lcm8gZXMgY2FsY3VsYXIgdW5hIHBydWViYSBkZSBpZ3VhbGRhZCBkZSB2YXJpYW56YXMgZW50cmUgbG9zIGdydXBvcywgbGxhbWFkYSBwcnVlYmEgZGUgTGV2ZW5lLgoKJCQKSF8wOiB2YXJfMSA9IHZhcl8yCiQkCgokJApIX2E6IHZhcl8xIOKJoCB2YXJfMgokJAoKIyMgUHJ1ZWJhIHQgcGFyYSBsYSBkaWZlcmVuY2lhIGRlIG1lZGlhcyBkZSB2aWN0aW1pemFjacOzbiBwb3IgY3JpbWVuIHBvciBnw6luZXJvCgpFbCBwcmltZXIgcGFzbyBlcyBoYWNlciBsYSBwcnVlYmEgZGUgTGV2ZW5lIHBhcmEgY29tcHJvYmFyIGxhIGlndWFsZGFkIG8gZGlmZXJlbmNpYSBkZSB2YXJpYW56YXMsIHF1ZSBlcyB1bmEgY29uZGljacOzbiBxdWUgbHVlZ28gc2UgdXNhIGVuIGxhIHBydWViYSB0LgpQYXJhIGNvcnJlciBlc3RlIHRlc3QsIHNlIHVzYSBsYSBsaWJyZXLDrWEgYERlc2NUb29sc2AsIHF1ZSBpbmNsdXllIGVsIGNvbWFuZG8gYExldmVuZVRlc3RgLgoKYGBge3IgbGV2ZW5lIGNyaW1lbn0KbGlicmFyeShEZXNjVG9vbHMpCkxldmVuZVRlc3QobGFwb3AyMSRjcmltZW4sIGxhcG9wMjEkZ2VuZXJvKQpgYGAKCkNvbW8gZWwgcC12YWx1ZSAoUHIoPkYpIGVzIG1lbm9yIGEgMC4wNSwgc2UgcmVjaGF6YSBsYSBoaXDDs3Rlc2lzIGNlcm8geSBzZSBhZmlybWEgcXVlIGxhcyB2YXJpYW56YXMgc29uIGRpZmVyZW50ZXMuCkNvbiBlc3RlIHJlc3VsdGFkbywgc2UgcHVlZGUgY29ycmVyIGVsIGNvbWFuZG8gYHQudGVzdGAsIGN1eWEgaGlww7N0ZXNpcyBjZXJvIGluZGljYSBxdWUgbGFzIG1lZGlhcyBkZSB2aWN0aW1pemFjacOzbiBwb3IgY3JpbWVuIHNvbiBpZ3VhbGVzIGVudHJlIGhvbWJyZSB5IG11amVyZXMgeSBsYSBoaXDDs3Rlc2lzIGFsdGVybmF0aXZhIGluZGljYSBxdWUgYW1iYXMgbWVkaWFzIHNvbiBkaWZlcmVudGVzLgpTZSBpbmNsdXllIGxhIGVzcGVjaWZpY2FjacOzbiBgdmFyLmVxdWFsPUZgIGRlYmlkbyBhbCByZXN1bHRhZG8gZGUgbGEgcHJ1ZWJhIGRlIExldmVuZSBxdWUgaW5kaWNhIHF1ZSBsYXMgdmFyaWFuemFzIHBhcmVjZW4gZGlmZXJlbnRlcy4KCmBgYHtyIHBydWViYSB0IGNyaW1lbn0KdC50ZXN0KGNyaW1lbiB+IGdlbmVybywgZGF0YSA9IGxhcG9wMjEsIHZhci5lcXVhbD1GKQpgYGAKCkVsIHZhbG9yIGRlbCBwLXZhbHVlIGVzIG1lbm9yIGEgMC4wNSwgY29uIGxvIHF1ZSBzZSByZWNoYXphIGxhIGhpcMOzdGVzaXMgbnVsYSB5IHNlIGFmaXJtYSBsYSBoaXDDs3Rlc2lzIGFsdGVybmF0aXZhIGRlIHF1ZSBsYXMgbWVkaWFzIGVudHJlIGFtYm9zIGdydXBvcyBzb24gZGlmZXJlbnRlcy4KQ29uIGVzdG8gc2UgY29uY2x1eWUgcXVlIGxvcyBob21icmVzIHJlcG9ydGFuIHVuYSBtYXlvciB2aWN0aW1pemFjacOzbiBwb3IgY3JpbWVuIHF1ZSBsYXMgbXVqZXJlcyBlbiB0b2RhIGxhIHJlZ2nDs24uCgojIyBQcnVlYmEgdCBwYXJhIGxhIGRpZmVyZW5jaWEgZGUgbWVkaWFzIGRlIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSBwb3IgZ8OpbmVybwoKRGUgbGEgbWlzbWEgbWFuZXJhIHF1ZSBlbiBlbCBjYXNvIGFudGVyaW9yLCBzZSBjb3JyZSBwcmltZXJvIGxhIHBydWViYSBkZSBMZXZlbmUgcGFyYSBjb21wcm9iYXIgbGEgaWd1YWxkYWQgbyBkaWZlcmVuY2lhIGRlIHZhcmlhbnphcy4KCmBgYHtyIExldmVuZSBhcG95byBwb3IgZ2VuZXJvfQpsaWJyYXJ5KERlc2NUb29scykKTGV2ZW5lVGVzdChsYXBvcDE4JGluZzRyLCBsYXBvcDE4JGdlbmVybykKYGBgCgpDb21vIGVsIHAtdmFsdWUgKFByKD5GKSBlcyBtZW5vciBhIDAuMDUsIHNlIHJlY2hhemEgbGEgaGlww7N0ZXNpcyBjZXJvIHkgc2UgYWZpcm1hIHF1ZSBsYXMgdmFyaWFuemFzIHNvbiBkaWZlcmVudGVzLgpDb24gZXN0ZSByZXN1bHRhZG8sIHNlIHB1ZWRlIGNvcnJlciBlbCBjb21hbmRvIGB0LnRlc3RgLCBjdXlhIGhpcMOzdGVzaXMgY2VybyBpbmRpY2EgcXVlIGxhcyBtZWRpYXMgZGUgYXBveW8gYSBsYSBkZW1vY3JhY2lhIHNvbiBpZ3VhbGVzIGVudHJlIGhvbWJyZSB5IG11amVyZXMgeSBsYSBoaXDDs3Rlc2lzIGFsdGVybmF0aXZhIGluZGljYSBxdWUgYW1iYXMgbWVkaWFzIHNvbiBkaWZlcmVudGVzLgpTZSBpbmNsdXllIGxhIGVzcGVjaWZpY2FjacOzbiBgdmFyLmVxdWFsPUZgIGRlYmlkbyBhbCByZXN1bHRhZG8gZGUgbGEgcHJ1ZWJhIGRlIExldmVuZSBxdWUgaW5kaWNhIHF1ZSBsYXMgdmFyaWFuemFzIHBhcmVjZW4gZGlmZXJlbnRlcy4KCmBgYHtyIHBydWViYSB0IGFwb3lvIHBvciBnZW5lcm8sIG1lc3NhZ2U9RkFMU0UsIHdhcm5pbmc9RkFMU0V9CnQudGVzdChpbmc0ciB+IGdlbmVybywgZGF0YSA9IGxhcG9wMTgsIHZhci5lcXVhbD1GKQpgYGAKCkVsIHZhbG9yIGRlbCBwLXZhbHVlICg0LjU5ZS0wOSkgZXMgbWVub3IgYSAwLjA1LCBwb3IgbG8gcXVlIHNlIHJlY2hhemEgbGEgaGlww7N0ZXNpcyBjZXJvIHkgc2UgYWZpcm1hIGxhIGFsdGVybmF0aXZhLCBsbGVnYW5kbyBhIGxhIGNvbmNsdXNpw7NuIHF1ZSBsYXMgZGlmZXJlbmNpYXMgc29uIGRpZmVyZW50ZXMgZW4gbGEgcG9ibGFjacOzbiBhbCA5NSUgZGUgY29uZmlhbnphLgoKIyMgUHJ1ZWJhIHQgcGFyYSBsYSBkaWZlcmVuY2lhIGRlIG1lZGlhcyBkZSBhcG95byBhIGxhIGRlbW9jcmFjaWEgcG9yIGdydXBvcyBkZSDDoW1iaXRvCgpVbiDDumx0aW1vIGVqZW1wbG8gZXMgZXZhbHVhciBsYSBkaWZlcmVuY2lhIGVuIGVsIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSBlbnRyZSDDoW1iaXRvIGRlIHJlc2lkZW5jaWEuClNlIGNvcnJlIGxhIHBydWViYSBkZSBMZXZlbmEuCgpgYGB7ciBMZXZlbmUgYXBveW8gcG9yIGFtYml0b30KTGV2ZW5lVGVzdChsYXBvcDE4JGluZzRyLCBsYXBvcDE4JGFtYml0bykKYGBgCgpOdWV2YW1lbnRlLCBlbCBwLXZhbHVlIGVzIG1lbm9yIGEgMC4wNSwgY29uIGxvIHF1ZSBzZSByZWNoYXphIGxhIGhpcMOzdGVzaXMgZGUgaWd1YWxkYWQgZGUgdmFyaWFuemFzLgpMdWVnbyBzZSBjb3JyZSBsYSBwcnVlYmEgdCBjb24gbGEgZXNwZWNpZmljYWNpw7NuIGRlIHZhcmlhbnphcyBkaWZlcmVudGVzLgoKYGBge3IgcHJ1ZWJhIHQgYXBveW8gcG9yIGFtYml0b30KdC50ZXN0KGluZzRyIH4gYW1iaXRvLCBkYXRhID0gbGFwb3AxOCwgdmFyLmVxdWFsPUYpCmBgYAoKQSBkaWZlcmVuY2lhIGRlIGxvcyBlamVtcGxvcyBhbnRlcmlvcmVzLCBlbiBlc3RhIGNvbXBhcmFjacOzbiBlbCBwLXZhbHVlIHRhbWJpw6luIGVzIG1lbm9yIGEgMC4wNSwgcG9yIGxvIHF1ZSBzZSByZWNoYXphIGxhIGhpcMOzdGVzaXMgY2VybyB5IHNlIGVuY3VlbnRyYSBxdWUgbGFzIGRpZmVyZW5jaWFzIGVuIGVsIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSBlbnRyZSBlbCDDoW1iaXRvIHVyYmFubyB5IHJ1cmFsIHNvbiBlc3RhZMOtc3RpY2FtZW50ZSBzaWduaWZpY2F0aXZhcyBhbCA5NSUgZGUgY29uZmlhbnphLgpUYWwgY29tbyBpbmRpY2EgZWwgcmVwb3J0ZSAiQ29uc2lkZXJhbmRvIGxhIHJlZ2nDs24gZW4gc3UgY29uanVudG8sIGVsIEdyw6FmaWNvIDEuNSBtdWVzdHJhIHJlbGFjaW9uZXMgZXN0YWTDrXN0aWNhbWVudGUgc2lnbmlmaWNhdGl2YXMgZW50cmUgY2luY28gdmFyaWFibGVzIGRlbW9ncsOhZmljYXMgeSBncnVwb3Mgc29jaW9lY29uw7NtaWNvcyAoZWR1Y2FjacOzbiwgcmlxdWV6YSwgcmVzaWRlbmNpYSB1cmJhbmEvcnVyYWwsIGfDqW5lcm8geSBlZGFkKSB5IGVsIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSIgKHAuIDEzKS4KRW4gZXN0YSBzZWNjacOzbiBoZW1vcyBjb21wcm9iYWRvIGVzdG9zIHJlc3VsdGFkb3MgZXN0YWTDrXN0aWNvcyBwYXJhIHZhcmlhYmxlcyBkZW1vZ3LDoWZpY2FzIGRlIGRvcyBncnVwb3MsIGNvbW8gZ8OpbmVybyB5IHJlc2lkZW5jaWEgdXJiYW5hL3J1cmFsLgoKIyBSZXN1bWVuCgpFbiBlc3RhIHNlY2Npw7NuIGhlbW9zIGRlc2NyaXRvIHkgZ3JhZmljYWRvLCBjb21vIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSwgcG9yIGdydXBvcyBkZSBvdHJhIHZhcmlhYmxlLgpQYXJ0aWVuZG8gZGUgbGEgY29tcGFyYWNpw7NuIGRlIGludGVydmFsb3MgZGUgY29uZmlhbnphLCBmb3JtYWxpemFtb3MgZXN0YSBjb21wYXJhY2nDs24gY29uIHVuYSBwcnVlYmEgZXN0YWTDrXN0aWNhLCBjb21vIGxhIHBydWViYSB0LCBwYXJhIGNvbmNsdWlyIHNpIGxhcyBkaWZlcmVuY2lhcyBlbnRyZSBncnVwb3Mgc29uIGVzdGFkw61zdGljYW1lbnRlIHNpZ25pZmljYXRpdmFzLgoKIyBDw6FsY3Vsb3MgaW5jbHV5ZW5kbyBlbCBlZmVjdG8gZGUgZGlzZcOxbwoKIyMgUGFyYSB2aWN0aW1pemFjacOzbiBwb3IgY3JpbWVuCgpQYXJhIGNhbGN1bGFyIGxhIGRpZmVyZW5jaWEgZGUgbWVkaWFzIGluY2x1eWVuZG8gZWwgZmFjdG9yIGRlIGV4cGFuc2nDs24gc2UgcHVlZGUgdXNhciBsYSBsaWJyZXLDrWEgYHN1cnZleWAuCkVzdGUgY29tYW5kbyByZXF1aWVyZSB1bmEgYWRlY3VhY2nDs24gZGUgbGEgYmFzZSBkZSBkYXRvcywgZGUgbGEgbWlzbWEgbWFuZXJhIHF1ZSBzZSBoaXpvIGVuIGVzdGUgW23Ds2R1bG9dKGh0dHBzOi8vYXJ0dXJvbWFsZG9uYWRvLmdpdGh1Yi5pby9CYXJvbWV0cm9FZHVfV2ViL0Rlc2NyaXB0aXZvczIuaHRtbCkuCgpgYGB7ciBwcmVwYXJhY2lvbiBkZSBiYXNlIDIxLCBlY2hvPVRSVUUsIG1lc3NhZ2U9RkFMU0UsIHdhcm5pbmc9RkFMU0UsIHJlc3VsdHM9J2hpZGUnfQpsYXBvcDIxID0gc3Vic2V0KGxhcG9wMjEsICFpcy5uYSh3ZWlnaHQxNTAwKSkKc2FwcGx5KGxhcG9wMjEsIGhhdmVuOjp6YXBfbGFiZWxzKQpgYGAKClVuYSB2ZXogYWRlY3VhZGEgbGEgYmFzZSBkZSBkYXRvcywgc2UgdGllbmUgcXVlIGRlZmluaXIgZWwgZGlzZcOxbyBtdWVzdHJhbCBjb24gZWwgY29tYW5kbyBgc3Z5ZGVzaWduYCB5IGd1YXJkYXIgZXN0ZSBkaXNlw7FvIGVuIHVuIG9iamV0bywgYXF1w60gbGxhbWFkbyAiZGlzZW5vMjEiLgoKYGBge3IgZGlzZW5vIDIxfQpsaWJyYXJ5KHN1cnZleSkKZGlzZW5vMjEgPSBzdnlkZXNpZ24oaWRzID0gfnVwbSwgc3RyYXRhID0gfnN0cmF0YSwgd2VpZ2h0cyA9IH53ZWlnaHQxNTAwLCBuZXN0PVRSVUUsIGRhdGE9bGFwb3AyMSkKYGBgCgpFbiBwcmltZXIgbHVnYXIsIHNlIHB1ZWRlIGNhbGN1bGFyIGxhIHRhYmxhIGRlIGxhIG1lZGlhIGRlIHZpY3RpbWl6YWNpw7NuIHBvciBjcmltZW4gcGFyYSBjYWRhIHZhbG9yIGRlIGxhIHZhcmlhYmxlIGfDqW5lcm8gaW5jbHV5ZW5kbyBlbCBmYWN0b3IgZGUgZXhwYW5zacOzbi4KRGUgbGEgbWlzbWEgbWFuZXJhIHF1ZSBzZSB2aW8gZW4gbGEgc2VjY2nDs24gc29icmUgW2ludGVydmFsb3MgZGUgY29uZmlhbnphXShodHRwczovL2FydHVyb21hbGRvbmFkby5naXRodWIuaW8vQmFyb21ldHJvRWR1X1dlYi9JQy5odG1sKSwgc2UgdXNhIGVsIGNvbWFuZG8gYHN2eWJ5YC4KCmBgYHtyIGNyaW1lbiBwb3IgZ2VuZXJvIHBvbmR9CmNyeGdlbi53IDwtIHN2eWJ5KH5jcmltZW4sIH5nZW5lcm8sIGRpc2VubzIxLCBzdnltZWFuLCBuYS5ybT1ULCB2YXJ0eXBlID0gImNpIikKY3J4Z2VuLncKYGBgCgpTZSBkZWJlIG5vdGFyIHF1ZSBlc3RvcyByZXN1bHRhZG9zIHNvbiBpZ3VhbGVzIGEgbG9zIHByZXNlbnRhZG9zIGVuIGVsIGdyw6FmaWNvIDMuMTIuCkNvbiBlc3RhIHRhYmxhIHNlIHB1ZWRlIHByb2NlZGVyIGEgcmVwbGljYXIgZWwgZ3LDoWZpY28gZGUgYmFycmFzIGRlbCBwYW5lbCBpenF1aWVyZG8gZGUgZXNlIGdyw6FmaWNvLCBkZSBsYSBtaXNtYSBtYW5lcmEgcXVlIHNlIHJlYWxpesOzIGFycmliYSBlbiBlc3RhIHNlY2Npw7NuLgoKUGFyYSBlbCBjw6FsY3VsbyBkZSBsYSBwcnVlYmEgdCBkZSBkaWZlcmVuY2lhIGRlIG1lZGlhcywgZWwgcGFxdWV0ZSBgc3VydmV5YCBjdWVudGEgY29uIHVuIGNvbWFuZG8gbmF0aXZvIHF1ZSBwZXJtaXRlIGhhY2VyIGVzdGUgY2FsY3VsbyBgc3Z5dHRlc3RgLgpTaW4gZW1iYXJnbywgZW4gZXN0ZSBjYXNvIG5vIHNlIGN1ZW50YSBjb24gdW4gY29tYW5kbyBwYXJhIGV2YWx1YXIgbGEgaWd1YWxkYWQgZGUgdmFyaWFuemFzLCBjb21vIGVsIGBMZXZlbmVUZXN0YC4KRWwgY29tYW5kbyBgc3Z5dHRlc3RgIGVzIHVuYSBkZXJpdmFjacOzbiBkZSB1biBjb21hbmRvIG3DoXMgZ2VuZXJhbCBwYXJhIG1vZGVsb3MgbGluZWFsZXMgZ2VuZXJhbGl6YWRvcywgcXVlIGFzdW1lbiBpZ3VhbGRhZCBkZSB2YXJpYW56YXMuClNpIHNlIHF1aXNpZXJhIGNvbXByb2JhciBlc3RlIHN1cHVlc3RvLCBzZSBwdWVkZSBoYWNlciBkZSBtYW5lcmEgbWFudWFsLCB0YWwgY29tbyBzZSBpbmRpY2EgZW4gZXN0ZSBbbGlua10oaHR0cHM6Ly9zdGF0cy5zdGFja2V4Y2hhbmdlLmNvbS9xdWVzdGlvbnMvMTQ4MzE0L2YtdGVzdC1mb3ItZXF1YWxpdHktb2YtdmFyaWFuY2VzLXdpdGgtd2VpZ2h0ZWQtc3VydmV5LWRhdGEpLgpBcXXDrSBzZSB2YSBhIHByb2NlZGVyIGFzdW1pZW5kbyBlbCBzdXB1ZXN0by4KU2Ugb2JzZXJ2YSBxdWUgZWwgY29tYW5kbyByZWdyZXNhIHJlc3VsdGFkb3MgbXV5IHBhcmVjaWRvcyBhbCBjb21hbmRvIHNpbiBlbCBlZmVjdG8gZGUgZGlzZcOxbyB5IHBhcmEgdG9kbyBlZmVjdG8gc2UgbGxlZ2FuIGEgbGFzIG1pc21hcyBjb25jbHVzaW9uZXMuCkVsIHAtdmFsdWUgZXMgbWVub3IgYSAwLjA1LCBwb3IgbG8gcXVlIHNlIHB1ZWRlIHJlY2hhemFyIGxhIEgwIGRlIGlndWFsZGFkIGRlIG1lZGlhcyB5IGFmaXJtYXIgcXVlIGV4aXN0ZSB1bmEgZGlmZXJlbmNpYSBlbiBlbCBhcG95byBhIGxhIGRlbW9jcmFjaWEgZW50cmUgaG9tYnJlcyB5IG11amVyZXMgZW4gbGEgcG9ibGFjacOzbiwgdG9tYW5kbyBlbiBjdWVudGEgZWwgZWZlY3RvIGRlIGRpc2XDsW8uCgpgYGB7ciBwcnVlYmEgdCBjcmltZW4gcG9yIGdlbmVybyBwb25kfQpzdnl0dGVzdChjcmltZW5+Z2VuZXJvLCBkaXNlbm8yMSkKYGBgCgpDb21vIGVsIHAtdmFsdWUgZXMgbWVub3IgYSAwLjA1LCBzZSBjb25jbHV5ZSBxdWUgZXhpc3RlbiBkaWZlcmVuY2lhcyBlbnRyZSBob21icmUgeSBtdWplcmVzIGVuIHN1cyBuaXZlbGVzIGRlIHZpY3RpbWl6YWNpw7NuIHBvciBlbCBjcmltZW4gZW4gdG9kYSBsYSByZWdpw7NuLgoKIyMgUGFyYSBhcG95byBhIGxhIGRlbW9jcmFjaWEKCkRlIGxhIG1pc21hIG1hbmVyYSBxdWUgZW4gZWwgZWplbXBsbyBhbnRlcmlvciwgZW4gcHJpbWVyIGx1Z2FyIHNlIGRlZmluZSBlbCBlZmVjdG8gZGUgZGlzZcOxbyB5IHNlIGd1YXJkYSBlbiB1biBvYmpldG8gImRpc2VubzE4Ii4KCmBgYHtyIHN1cnZleSwgbWVzc2FnZT1GQUxTRSwgd2FybmluZz1GQUxTRX0KbGlicmFyeShzdXJ2ZXkpCmRpc2VubzE4PC1zdnlkZXNpZ24oaWRzID0gfnVwbSwgc3RyYXRhID0gfmVzdHJhdG9wcmksIHdlaWdodHMgPSB+d2VpZ2h0MTUwMCwgbmVzdD1UUlVFLCBkYXRhPWxhcG9wMTgpCmBgYAoKTHVlZ28sIHNlIHVzYSBlbCBjb21hbmRvIGBzdnlieWAgcGFyYSBjYWxjdWxhciBsYSBtZWRpYSBkZSBhcG95byBhIGxhIGRlbW9jcmFjaWEgcG9yIGdydXBvcyBkZSBnw6luZXJvLgoKYGBge3IgdGFibGF3ZWlnaHRlZH0KYXB4Z2VuLncgPC0gc3Z5YnkofmluZzRyLCB+Z2VuZXJvLCBkaXNlbm8xOCwgc3Z5bWVhbiwgbmEucm09VCwgdmFydHlwZSA9ICJjaSIpCmFweGdlbi53CmBgYAoKQ29uIGVzdGEgdGFibGEgc2UgcHVlZGUgcHJvY2VkZXIgYSBjcmVhciBlbCBncsOhZmljbyBkZSBiYXJyYXMsIGRlIGxhIG1pc21hIG1hbmVyYSBxdWUgc2UgcmVhbGl6w7MgYXJyaWJhIGVuIGVzdGEgc2VjY2nDs24uCgpJZ3VhbCBxdWUgZW4gZWwgZWplbXBsbyBhbnRlcmlvciwgc2UgcHJvY2VkZSBhIHVzYXIgZWwgY29tYW5kbyBuYXRpdm8gYHN2eXR0ZXN0YCBwYXJhIGV2YWx1YXIgbGEgZGlmZXJlbmNpYSBkZSBtZWRpYXMgZGUgYXBveW8gYSBsYSBkZW1vY3JhY2lhIGVudHJlIGhvbWJyZXMgeSBtdWplcmVzLgoKYGBge3IgdHdlaWdodGVkfQpzdnl0dGVzdChpbmc0cn5nZW5lcm8sIGRpc2VubzE4KQpgYGAKCkNvbW8gZWwgcC12YWx1ZSBlcyBtZW5vciBhIDAuMDUsIHNlIGNvbmNsdXllIHF1ZSBzw60gZXhpc3RlbiBkaWZlcmVuY2lhcyBlbnRyZSBob21icmUgeSBtdWplcmVzIGVuIGVsIGFwb3lvIGEgbGEgZGVtb2NyYWNpYSBlbiB0b2RhIGxhIHJlZ2nDs24uCg==




